Resultats de la cerca
Es mostren 5 resultats
àlgebra de Lie
Matemàtiques
Estructura algebraica l’ús principal de la qual resideix en l’estudi d’objectes geomètrics com ara grups de Lie i varietats diferenciables.
Àlgebra E tal que la seva llei de composició x , y compleix les dues propietats següents per a tot x ∈ E , x , x = 0 i, per a cada terna x , y , z ∈ E , x , y , z + y , z , x + z , x , y = 0 Un exemple d’àlgebra de Lie el constitueix l’espai ℝ 3 dotat del producte vectorial L’estudi d’aquestes àlgebres és important per a l’estudi dels grups de Lie, ja que, a cada grup de Lie, se li pot associar una àlgebra de Lie
graf
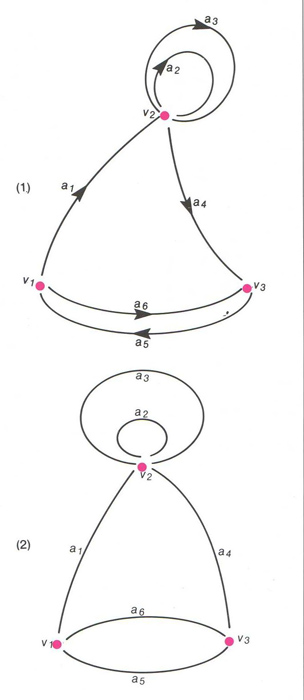
(1) Graf orientat: el camí ( a 1, a 2, a 4, a 5) és un circuit , els arcs a 2 i a 3 són bucles o rulls en el vèrtex v 2. i a 6 és un camí de v 1 a v 3. (2) graf no orientat: la cadena ( a 1, a 4, a 5) és un cicle , les arestes a 2 i a 3 són bucles o rulls en el vèrtex v 2, i a 6 és una aresta de v 1 a v 3.
© fototeca.cat
Matemàtiques
Ens constituït per un conjunt S
d’elements i per un conjunt C
de línies que uneixen els elements de S
(tot palesant una correspondència
de S
en si mateix).
Cal distingir entre un graf orientat i un graf no orientat Un graf orientat és una quaterna S, C, o, e , on S és el conjunt d’elements o vèrtexs, C és el conjunt de línies entre els vèrtexs o arcs, o és l' aplicació origen que assigna a cada arc el vèrtex del qual surt, i e és l' aplicació extrem que assigna a cada arc el vèrtex al qual arriba Un graf no orientat és una terna S, C, e , on S és el conjunt dels vèrtexs, C és el conjunt de línies entre els vèrtexs o arestes , i e és l’aplicació que assigna a cada aresta una parella de S × S , formada pels vèrtexs que uneix l’…
quadrangle
Matemàtiques
Figura formada per les sis rectes que determinen quatre punts, en els quals cap terna d’aquests no és alineada.
mesura
Matemàtiques
Aplicació m definida entre una àlgebra de conjunts ɑ d’un espai mesurable (Ω, ɑ) i el conjunt ℝ+ dels nombres reals positius.
L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑ és igual a la suma de les respectives mesures, és a dir ∀ A ∈ ɑ i ∀ B ∈ ɑ tals que A ∩ B = ∅, m A + m B La terna Ω, ɑ, m és anomenada espai de mesura , i els conjunts de l’àlgebra ɑ són anomenats mesurables En el cas que ɑ sigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑ disjunts dos a dos és igual a la suma de les respectives mesures, és a dir essent A i ∈ ɑ i A i ∩ A j = ∅, per a tot i, j tals que i ≠ j Una mesura és anomenada fitada…