Resultats de la cerca
Es mostren 16 resultats
nombre algèbric
Matemàtiques
Nombre que és solució d’una equació algèbrica racional.
El conjunt dels nombres algèbrics és numerable
algebraic | algebraica
teorema d’Hermite
Matemàtiques
Teorema que afirma que el nombre e és un nombre transcendent.
Fou demostrat per ChHermite el 1873 L’extensió del teorema, que afirma que per a qualsevol nombre algèbric α, el nombre e α és un nombre transcendent, és conegut com a teorema d’Hermite-Lindemann
teoria de categories
Matemàtiques
Teoria introduïda cap al 1940 pels matemàtics S. Eilenberg i S. MacLane, fonamentada sobre el concepte de categoria, i aplicada inicialment en la topologia algèbrica.
És utilitzada en tot aquell tipus de problema algèbric on hom té una estructura de base i un conjunt de propietats genèriques que no depenen de la realització en un objecte matemàtic concret, especialment en àlgebra homològica i geometria algèbrica
lògica algèbrica
Matemàtiques
Estudi algèbric de la lògica com a llenguatge (metallenguatge).
La lògica algèbrica tracta, doncs, les estructures que presenten les diferents lògiques i d’aquesta manera arriba a trobar estructures algèbriques —poc usuals en l’àmbit de l’àlgebra clàssica— com són, entre d’altres, les àlgebres de Hilbert, de Heyting, d’Abbott, de Boole, de Wajsberg, monàdiques, poliàdiques i cilíndriques
recta
Matemàtiques
Línia que en l’espai ordinari dóna la distància més curta entre dos punts; la imatge material més simple és la donada per un cordill tibant.
En realitat aquesta imatge correspon millor a un segment o tros de recta la recta és, de fet, infinita en tots dos sentits La geometria no dóna cap definició directa de recta, sinó que, en fixar l’axiomàtica o conjunt de proposicions bàsiques de les quals hom dedueix totes les altres que constitueixen les diverses geometries, resten definits indirectament els conceptes fonamentals punt, recta, pla L’intent de definir cada element a partir d’altres de més simples no pot prosseguir indefinidament sense caure en un cercle viciós, puix que algun element ha d’ésser el primer d’aquesta cadena En el…
nombre transcendent
Matemàtiques
Nombre real no algèbric; per exemple e, π, els nombres de Liouville, etc.
v
Matemàtiques
Símbol algèbric emprat per a indicar màxim, com ara 5 v 2 = 5.
sistema de coordenades
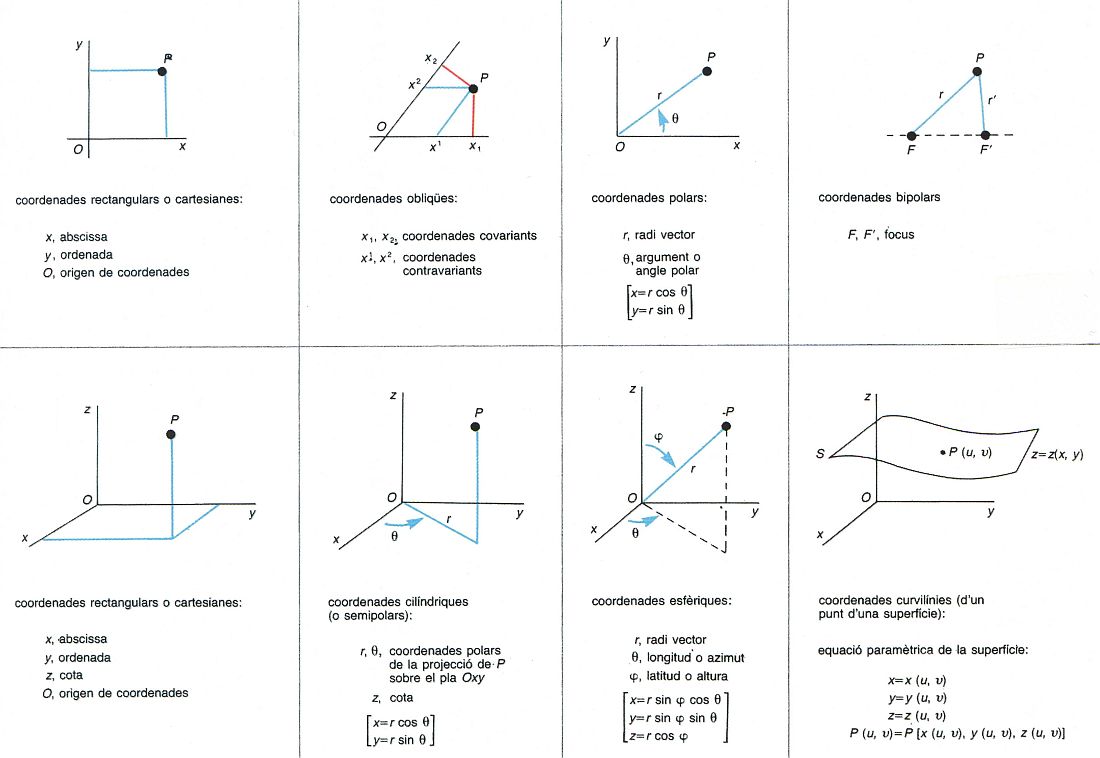
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot considerar les coordenades covariants o contravariants , que…
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…