Resultats de la cerca
Es mostren 323 resultats
casquet esfèric
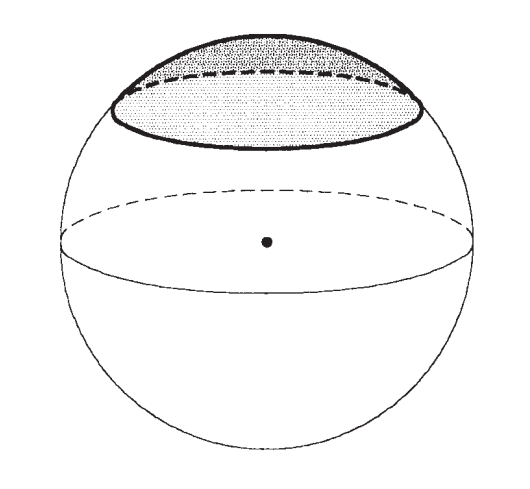
casquet esfèric
Matemàtiques
Cadascuna de les dues parts en què un pla divideix una superfície esfèrica.
Hom el pot considerar com una zona esfèrica d’una sola base un dels dos plans és tangent a l’esfera
Menelau d’Alexandria
Matemàtiques
Matemàtic grec.
Fou el primer a separar la trigonometria de l’estereometria i l’astronomia Féu la primera definició de triangle esfèric i utilitzà la relació entre els triangles esfèrics i els plans per a resoldre els triangles esfèrics teorema de Menelau Escriví el tractat Esfèrica , on establí els fonaments de la trigonometria esfèrica
potencial nuclear central
Física
Potencial nuclear amb simetria esfèrica.
La seva energia potencial depèn únicament de la distància al centre del camp
baló
Recipient de vidre de forma esfèrica.
superfície
Matemàtiques
Conjunt de punts de l’espai que poden ésser determinats per dos paràmetres.
La manera més simple de determinar una superfície és donar una o més equacions del tipus z = f x,y Elegit un punt x,y en el domini de definició de la funció f , aquesta funció o aquestes funcions donen els valors de z , que, juntament amb x,y , són les coordenades cartesianes dels punts de la superfície Les funcions que donen la superfície esfèrica són , on el signe + correspon a l’hemisferi superior, i el signe - a l’hemisferi inferior L’equació z = ax + by + c correspon al pla o superfície plana Sovint és difícil, o impossible, d’expressar una superfície per mitjà de les…
triangle esfèric
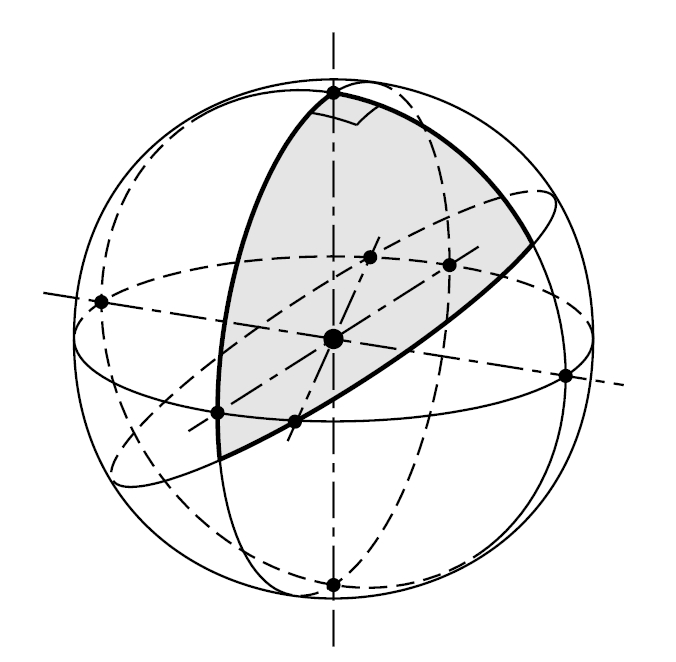
Triangle esfèric, amb un angle recte
Matemàtiques
Triangle curvilini format per tres cercles màxims d’una esfera.
L’estudi i la resolució d’aquests triangles constitueixen l’objectiu bàsic de la trigonometria esfèrica
dioptre
Física
Superfície que separa dos medis transparents de diferent índex de refracció.
Segons que la superfície sigui plana o esfèrica, hom parla de dioptres plans o de dioptres esfèrics
loxodromia
Matemàtiques
En una superfície de revolució, corba de la superfície que forma amb les generatrius un angle constant.
Tenen una especial importància les loxodromies d’una superfície esfèrica, perquè permeten d’aplicar aquest concepte a la superfície de la Terra