Resultats de la cerca
Es mostren 79 resultats
mètode de racionalització de Gauss
Matemàtiques
Algorisme emprat en l’estudi dels espais vectorials que, donats uns vectors arbitraris, permet de deduir-ne efectivament els que són linealment independents i que, per tant, també són base del subespai que generen.
Hom aplica aquest mètode per a trobar el rang d’una matriu qualsevol no necessàriament quadrada, considerant cada fila de la matriu com un vector
Principi de dualitat (Poncelet, Plücker, Gergonne); funcions el·líptiques (Abel, Gauss, Jacobi).
Principi de dualitat Poncelet, Plücker, Gergonne funcions ellíptiques Abel, Gauss, Jacobi
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes (Gauss)
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes Gauss
llei normal
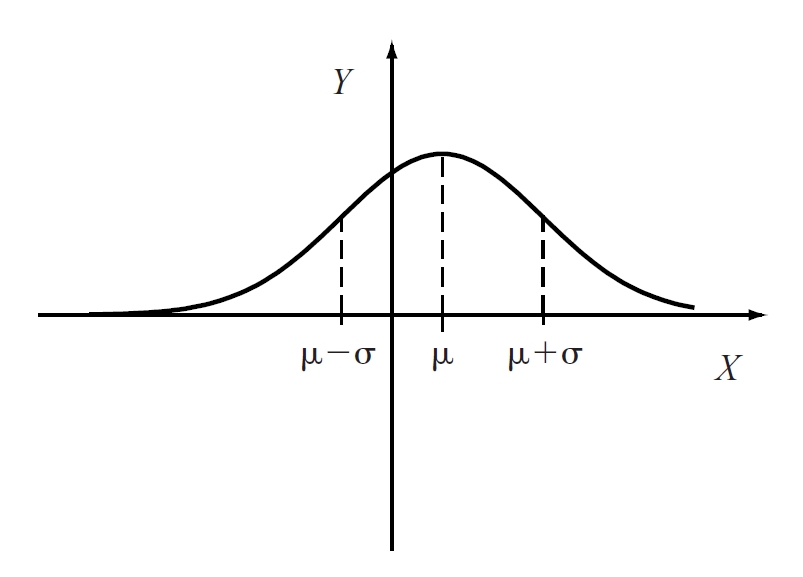
Llei normal de probabilitat de mitjana μ i desviació tipus σ
Fototeca.cat
Matemàtiques
Llei de probabilitat contínua i simètrica en la qual la mitjana, la moda i la mediana coincideixen i la funció de densitat té forma de campana de Gauss o corba normal.
Aquesta densitat depèn de dos paràmetres, la mitjana μ i la desviació típica σ En general, es caracteritza per N μ, σ i la seva funció de densitat val
Wilhelm Eduard Weber

Wuilheim Eduard Weber
© Fototeca.cat
Física
Físic alemany.
Fou professor a Halle i Göttingen Són especialment importants els seus estudis sobre l’electricitat i el magnetisme Amb Gauss estudià el magnetisme terrestre i inventà un telè- graf electromagnètic 1833 Construí també un electrodinamòmetre i proposà, amb Gauss, un sistema d’unitats en electricitat També féu estudis sobre acústica i elaborà un sistema de compensació de temperatura per als tubs d’orgue Germà de germà d’ Ernst Heinrich Weber
pla complex
Matemàtiques
Pla de ℝ 2
obtingut mitjançant la identificació dels punts < x
, y
> amb els nombres complexos x
+ iy
.
Aquest pla rep també el nom de pla de Gauss o de Gauss-Argand Un punt z = < x , y > admet una representació en coordenades polars i, per tant, z = ρ ⋅ cos θ + i ⋅ sin θ que, d’acord amb la identitat d’Euler, hom escriu z = ρ ⋅ e i⋅θ Aquesta expressió permet de calcular amb facilitat les potències dels nombres complexos i extreure'n les seves arrels n -èsimes Resulta aleshores que la fórmula de Moivre s’expressa
Julius Wilhelm Richard Dedekind

Julius Wihelm Richard Dedekind
© Fototeca.cat
Matemàtiques
Matemàtic alemany, deixeble de Gauss.
Professor al politècnic de Zuric 1858 i a la Technische Hochschule de Brunsvic 1862-1912, ha estat un dels capdavanters de dos dels corrents bàsics que han donat origen i suport a la matemàtica moderna el formalista culminat en l’obra de Hilbert, que bandeja qualsevol possibilitat d’incloure un raonament basat en la intuïció dins l’edifici matemàtic, i el logicista Was sind und was sollen die Zahlen , ‘Què són i per a què serveixen els nombres', 1888, que pretén de situar la matemàtica com a branca particular de la lògica, elaborat fins a les darreres conseqüències per Russell Construí una…
nombre complex
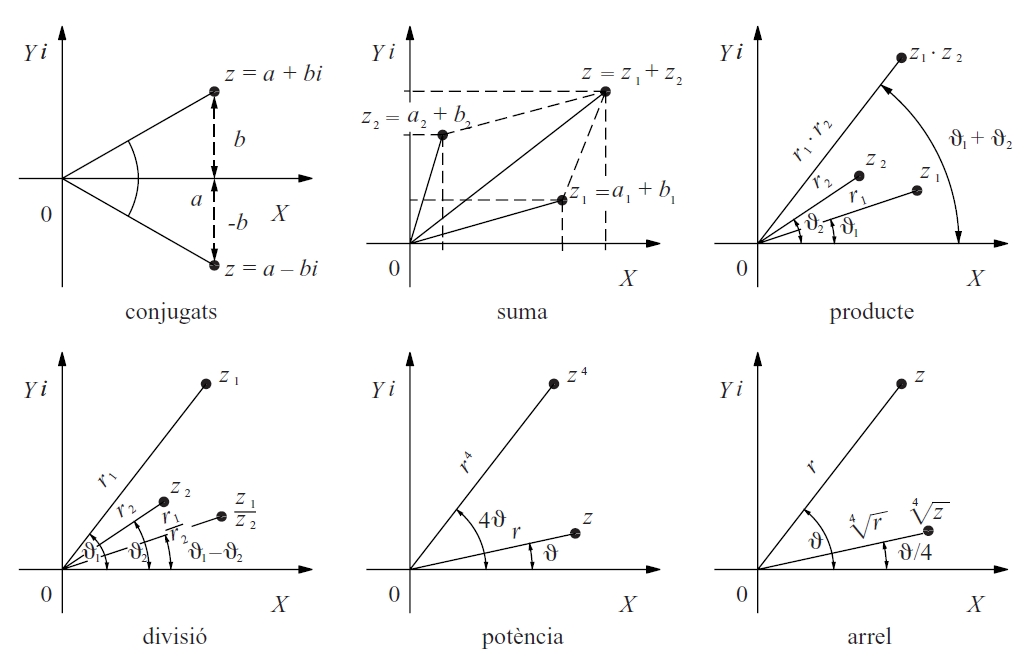
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…