Resultats de la cerca
Es mostren 64 resultats
antiprisma
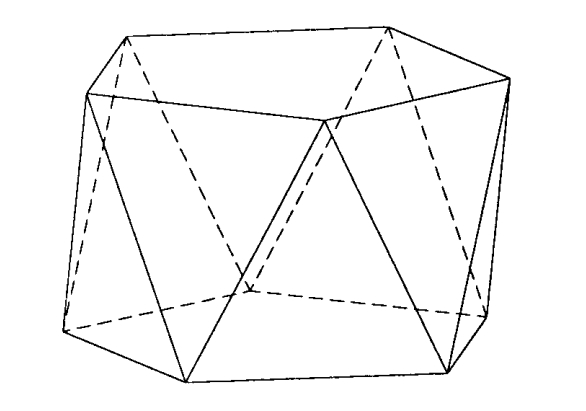
Antiprisma pentagonal
© Fototeca.cat
Matemàtiques
Poliedre format per dues bases, que són polígons congruents paral·lels però girats entre sí, i per cares laterals, que són triangles que resulten d’unir cada vèrtex d’una base amb els dos vèrtexs corresponents de l’altra base.
L’antripisma s’anomena triangular, quadrangular, etc si les bases són, respectivament, triangles, quadrilàters, etc L’octaedre és un antiprisma que és poliedre regular
piràmide
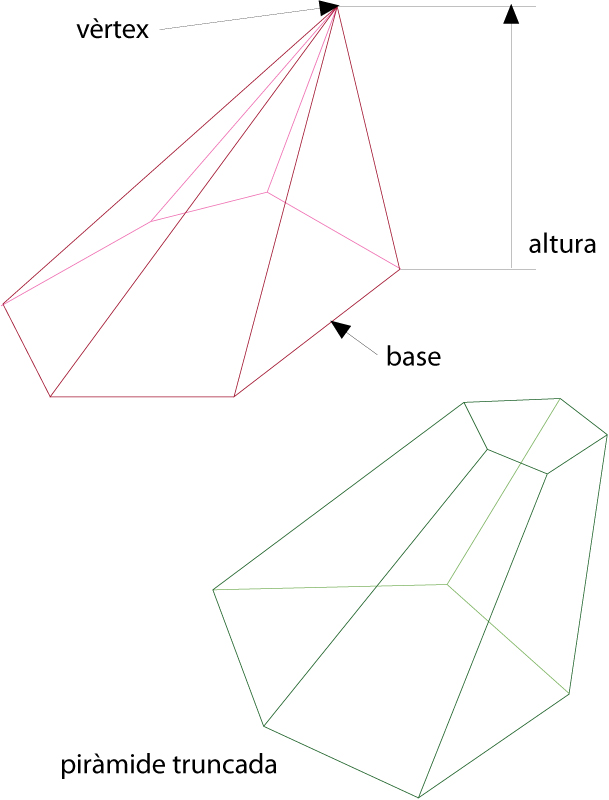
Piràmide irregular de base hexagonal i piràmide truncada de base pentagonal
© Fototeca.cat
Matemàtiques
Políedre que té per base un polígon qualsevol i les altres cares del qual (anomenades cares de la piràmide) són triangles que tenen un vèrtex comú (anomenat vèrtex de la piràmide).
Una piràmide és anomenada triangular tetràedre, quadrangular, pentagonal , etc, segons que la base sigui, respectivament, un triangle, un quadrilàter, un pentàgon, etc Una piràmide és anomenada regular si la base és un polígon regular i les cares són triangles isòsceles Hom anomena altura d’una piràmide la distància del vèrtex al pla del polígon El volum de la piràmide és el terç de la superfície de la base per l’altura Tallant una piràmide amb un pla hom obté dos políedres El políedre que conté el vèrtex és també una piràmide L’altre rep el nom de piràmide truncada
circumscriure
Matemàtiques
Traçar una figura que n’envolti una altra amb la qual tingui el major nombre de punts comuns possible.
Generalment hom circumscriu una corba superfície tancada a un polígon políedre que hi és contingut
paral·lelepípede
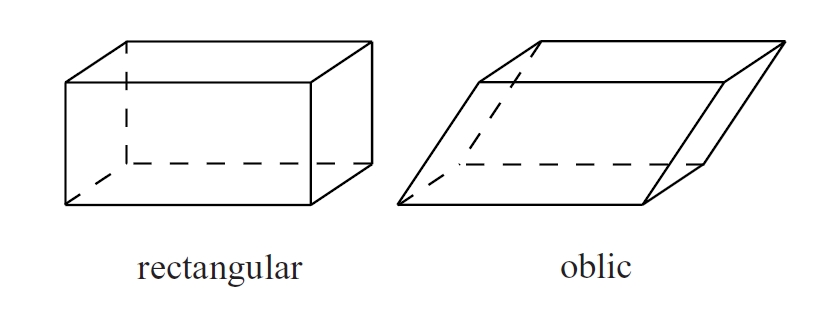
Paral·lelepípede
Matemàtiques
Prisma de sis cares, totes elles paral·lelograms.
Quan el prisma és recte i totes les cares són rectangles, és anomenat ortòedre L’ hexàedre és l’únic parallelepípede que és políedre regular
polítop
Matemàtiques
Conjunt de punts de l’espai ℝn limitat per hiperplans.
La noció de politop generalitza la de polígon i la de políedre De fet, els politops de ℝ 2 són els polígons i els politops de ℝ 3 són els políedres Un exemple de politop a ℝ 4 és el tesseractis , que és l' hipercub de quatre dimensions
sistema triclínic
Mineralogia i petrografia
Sistema cristal·lí format per dues classes de simetria, la característica de les quals és la manca de simetria.
Els eixos cristallogràfics són les arestes del políedre fonamental aquests no tenen cap angle igual, ni entre ells ni a 90° α ≠ β ≠ γ ≠90° La cara fonamental talla els tres eixos a distàncies desiguals, la seva relació essent paramètrica a ≠ b ≠ c Les formes simples d’aquest sistema són únicament pinacoides i pedions , formats respectivament per parelles de cares paralleles o per una sola cara Les plagiòclasis cristallitzen en aquest sistema
sistema cúbic
Mineralogia i petrografia
Sistema cristal·lí format per cinc classes cristal·lines que tenen en comú el fet de posseir quatre eixos ternaris equidistants els uns dels altres i que originen tres eixos binaris perpendiculars entre ells i equidistants dels anteriors, amb els quals formen angles de 54°44’.
Els tres eixos binaris esdevenen quaternaris en les dues classes de més simetria del sistema El políedre fonamental és el cub o hexàedre, integrat per sis cares equivalents i perpendiculars amb els eixos quaternaris Les arestes són els eixos cristallogràfics del sistema, els quals s’intersequen perpendicularment α = β = γ = 90° La forma que determina la relació paramètrica és l’octàedre en el qual les cares són perpendiculars als eixos ternaris i determinen paràmetres iguals sobre els eixos cristallogràfics a b c = 111 = 1 Hom el coneix també amb el nom de sistema regular