Resultats de la cerca
Es mostren 1547 resultats
matriu
Matemàtiques
Disposició dels elements d’un cos K
de la manera següent
.
Segons que el cos K sigui el dels nombres reals o el dels nombres complexos, hom parla de matriu real o de matriu complexa , respectivament Cadascuna de les línies horitzontals de nombres és una fila de la matriu, i cada línia vertical de nombres n'és una columna En l’exemple donat, la matriu A té files i columnes hom diu que A és una matriu m × n El conjunt de les matrius m ×és notat per M m X n K Una matriu pot ésser expressada també mitjançant el seu element genèric a i j , en la forma A = a i j Aquí, és l' índex de fila i j és l' índex de columna La fila…
distribució gamma
Matemàtiques
Llei de probabilitat de la variable contínua x, la funció de densitat de la qual és f(x) = e- xxk - 1/Γ(k) (0 < x < ∞;k > 0).
D’aquesta llei deriven algunes expressions particulars, com la llei X 2 i la llei d’Erlang Tendeix cap a la llei normal quan k augmenta indefinidament
Boris Solomonovic Steinpress
Música
Musicòleg ucraïnès.
Estudià piano i musicologia al Conservatori de Moscou El 1938 obtingué el doctorat amb una dissertació sobre Les noces de Fígaro , de WA Mozart Impartí la docència als conservatoris de Moscou 1931, 1933-36 i de Sverdlovsk 1936-37, 1942-43 i a l’Institut d’Educació Musical a distància d’aquesta ciutat, centre d’on fou cap del departament d’història de la música i degà A partir del 1926 també es dedicà a la crítica En els seus escrits s’ocupà especialment de la vida musical russa, la història de la música zíngara, les biografies de compositors com AA Al’abjev, N Rimskij-Korsakov, M Glinka i A…
subcòs
Matemàtiques
Qualsevol subconjunt L d’un cos K tal, que és estable per les dues operacions de K i, mitjançant aquestes restriccions, L té també una estructura de cos.
L és subcòs del cos K si L és un subanell unitari tal, que l’invers de tot element no nul de L pertany a L El conjunt de nombres racionals és un subcòs del conjunt de nombres reals el qual té estructura de cos
deltoide
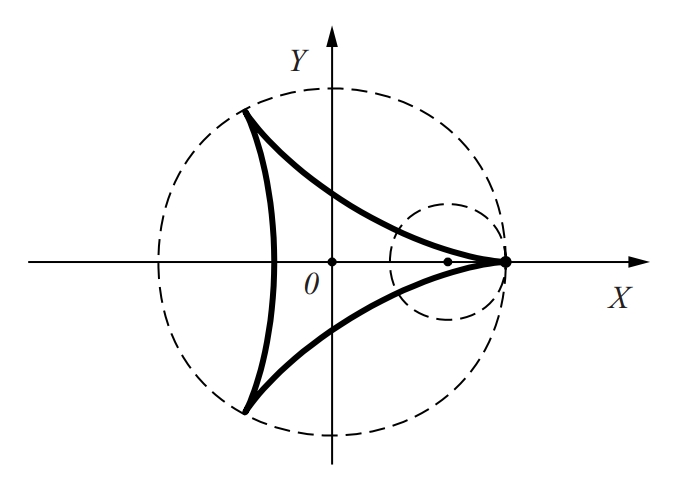
deltoide
Matemàtiques
Hipocicloide d’un cercle de radi k que roda, sense lliscar, dintre d’un altre que té el radi triple.
Les seves equacions paramètriques són x = k 2cos t + cos 2t , i y = k 2sin t + sin 2 t
mètode dels multiplicadors de Lagrange
Matemàtiques
Mètode per a trobar els màxims o mínims d’una funció u = F(x1, x2,..., xn) de n variables, les quals són sotmeses a k condicions suplementàries φ1(x1, x2,..., xn) = 0, φ2(x1, x2,..., xn) = 0,..., φk(x1, x2,..., xn) = 0.
, x n = 0, φ 2 x 1 , x 2 ,, x n = 0,, φ k &x 1 , x 2 ,, x n = 0 El mètode consisteix a formar la funció + λ 2 φ 2 x 1 ,, x n + λ 2 φ 2 > x 1 ,, x n , + + λ k φ k x 1 ,, x n , on λ 1 ,, λ k són constants indeterminades, anomenades multiplicadors de Lagrange les n derivades parcials de ϕ igualades a 0 juntament amb les k condicions constitueixen un sistema de n + k equacions i n + k incògnites λ 1 ,, λ k , x 1 , , x n Atès que aquest sistema constitueix només una condició…
Katy Mayr Lubillo

Katy Mayr Lubillo
ARXIU K. MAYR / J. CID
Natació
Nedadora de salvament i socorrisme.
Membre del Club Natació Catalunya des del 1965, participà en un Campionat d’Espanya de natació i en diversos torneigs catalans, com la Copa Nadal i les travessies a l’estany de Banyoles i els ports de Barcelona i Tarragona El 1967 s’inicià en salvament aquàtic i obtingué el títol de socorrista Participà en nombrosos Campionats d’Espanya i de Catalunya i en tres Campionats del Món 1967, 1968, 1969 Guanyà la medalla de bronze en 200 m natació amb obstacles en el Campionat del Món 1968 En la mateixa competició assolí dues medalles per equips, una de bronze 1968 i una d’or 1969 Posteriorment fou…
Triglav

Vista del Triglav
© Slovenian Tourist Board / K. Kunaver
Muntanya
Muntanya dels Alps Julians, a Eslovènia, prop de la frontera amb Àustria i amb Itàlia (2 863 m).
Hi neix el Sava
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F…
fórmula de Boltzmann
Física
Expressió que relaciona l’entropia S d’un sistema (magnitud macroscòpica) i el nombre d’estats microscòpics accessibles pel sistema, W (magnitud microscòpica): S = k lnW, essent k la constant de Boltzmann.
Palesa la connexió entre la termodinàmica clàssica i la mecànica estadística Al zero absolut T = 0 K totes les partícules del sistema són a l’estat fonamental, de manera que W = 1 i, per tant, S = 0, la qual cosa és d’acord amb el tercer principi de la termodinàmica teorema de Nernst
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- …
- Pàgina següent
- Última pàgina