Resultats de la cerca
Es mostren 34898 resultats
oposició significativa
Fonètica i fonologia
Lingüística i sociolingüística
Oposició formada per dos signes de la llengua, els significats dels quals són diferents.
Així, en llatí equus / equīs , dominus / equus En tractar-se de dos signes, resta implícit en la definició que els significants han d’ésser també diferents Algunes de les oposicions significatives són simplement oposicions de vocabulari , mentre que d’altres sómn oposicions gramaticals
bosons vectorials
Física
Bosons de spin unitat que, per tant, són descrits mitjançant una funció d’ona vectorial.
Són el fotó, les partícules W + , W - i Z° i els gluons
mesó
Física
Hadró amb spin enter (0, 1, 2,...); els mesons són, doncs, hadrons bosònics.
Tenen nombre bariònic 0 Les primeres classificacions de les partícules subatòmiques foren fetes atenent la massa els mesons tenien una massa compresa entre la dels leptons i la dels barions En l’actual model de quarks, un mesó és un hadró constituït d’un quark i un antiquark quark La seva existència fou predita per Yukawa, el 1935, per tal d’explicar la natura de les forces nuclears, de les quals els feia responsables Hom coneix més de 60 mesons, tots ells inestables Són mesons els pions i els kaons , per exemple
Marx
Cinematografia
Nom amb què són coneguts els germans Marks, actors cinematogràfics nord-americans.
La família fou composta per Leonard Nova York 1891 — 1961 “Chico”, Arthur Nova York 1893 — 1964 “Harpo”, Julius Nova York 1895 — Los Angeles 1977 “Groucho”, Milton Nova York 1894 — Palm Springs, Califòrnia 1977 “Gummo” i Herbert Nova York 1901— Palm Springs, Califòrnia 1979 “Zeppo” Tot i que en algun moment treballaren plegats, només Chico, Harpo i Groucho formaren l’equip que tingué una projecció internacional Les escenes jocoses, d’una comicitat desllorigada, agressiva i carregada d’una crítica —bàsicament social— implacable, són completades per aquelles en què Chico —pianista— i Harpo —…
perciformes
Ictiologia
Ordre de peixos de la subclasse dels osteïctis, que tenen les aletes dorsals dotades d’un cert nombre de radis espinosos situats en posició anterior, les aletes pectorals són situades força amunt, i les ventrals, si existeixen, són en posició toràcica.
Són fisoclists És l’ordre de peixos més ampli i més evolucionat filogenèticament Comprèn 125 famílies, 40 de les quals són representades a la Mediterrània
oposició
Astronomia
Situació relativa de dos astres quan són alineats amb la Terra i aquesta és entre tots dos.
Quan dos astres són en oposició, entre les longituds geocèntriques de l’un i de l’altre hi ha una diferència de 180°, i entre les ascensions rectes coordenades astronòmiques hi ha una diferència de 12 h Quan un planeta superior és en oposició amb el Sol, la seva culminació té lloc a mitjanit i, per tant, les condicions d’observació dels planetes són òptimes Els planetes inferiors mai no poden ésser en oposició amb el Sol elongació
relació transitiva
Matemàtiques
Relació R en un conjunt A tal, que si a i b són relacionats per R (a R b) i b, c també ho són (b R c), aleshores entre a i c també hi ha la mateixa relació.
Les relacions numèriques d’igualtat o la relació “ésser multiple de” són transitives Les relacions d’equivalència i ordre també ho són Relacions com la d’"ésser amic” o “ésser pare de”, per contra, no ho compleixen Tota relació transitiva i reflexiva tot element és relacionat amb ell mateix, a R a és dita preordre
verticil·lastre
Botànica
Conjunt de flors que, agrupades en cimes de peduncles curts, són situades a un mateix nivell.
Els verticillastres són típics de les labiades
tolteca

Chac mool tolteca, trobat a l’antiga ciutat tolteca de Tula, Mèxic. Els Chac mool són unes escultures antropomòrfiques emprades en les cerimònies rituals de sacrifici.
© Corel Professional Photos
Etnologia
Història
Individu d’un poble amerindi precolombí pertanyent probablement al grup nahua que desenvolupà a Mèxic una de les cultures postclàssiques més importants (segles IX-XII).
El seu caràcter guerrer i militarista es reflectia en l’organització de castes i, sobretot, en la religió Texcatlipoca, déu guerrer, obligava a una guerra constant per tal de satisfer la seva necessitat de víctimes hom li sacrificava els presoners A la seva capital, Tula, fou imposat temporalment el culte del pacífic Quetzalcóatl dels teotihuacans Els seus devots foren expulsats al Yucatán, on donaren nova esplendor a Chichén Itzá Derrotats 1168 pels txitximeques es refugiaren a Txolula i a Calhuacan Els asteques foren uns hereus de llur cultura
corrent del Golf
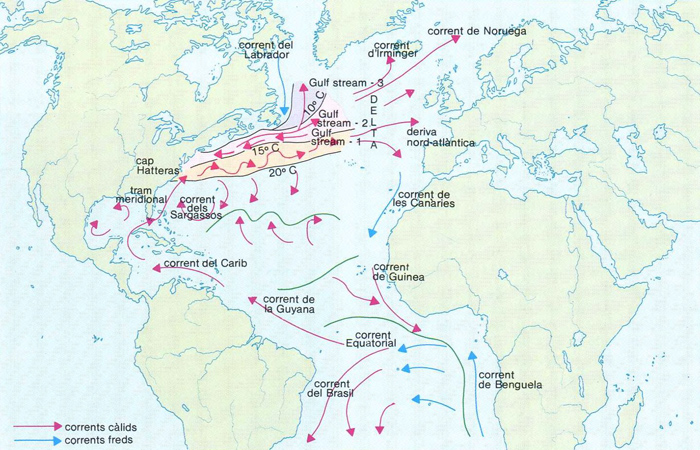
Els tres segments del tram septentrional són indicats en colors diferents i limitats per les corbes isotermes. En el delta del corrent del Golf s’originen els altres corrents de l’Atlàntic Nord
© fototeca.cat
Corrent marí de l’hemisferi boreal, a l’Atlàntic occidental.
La raó última del seu enorme cabal el segon del món en importància és la tendència del sistema hidrològic del planeta a disminuir el desequilibri tèrmic entre les zones tropicals i les polars les pecualiaritats del corrent depenen de la geografia de la conca afectada i de la interacció amb la resta de corrents marins de la zona El corrent és compost de dos trams principals, un de meridional i un de septentrional El tram meridional és originat quan a les aigües càlides a una mitjana de més de 25°C i ràpides, que surten del Golf de Mèxic cap a l’Atlàntic accelerades pel canal de Florida, s’…
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- …
- Pàgina següent
- Última pàgina