Resultats de la cerca
Es mostren 681 resultats
funció multiforme
Matemàtiques
Funció que assigna diverses imatges a cada element del domini de definició.
En són exemple les funcions trigonomètriques inverses arc sin1 = {π/2, π/2+2π, π/2+4π,,π/2+2 n π,} Les funcions multiformes no són, en el sentit estricte del terme funcions , sinó correspondències Una funció multiforme esdevé una funció quan hom n'escull una branca o determinació per exemple, la funció Arc sin x és la branca de la funció multiforme arc sin x definida en restringir a 0,2π el recorregut d’aquesta
Lingüística 2019
Lingüística i sociolingüística
L’any 2019 va ser un any atapeït d’esdeveniments polítics, socials i culturals als diferents territoris de parla catalana A Catalunya , en l’apartat judicial, el Tribunal Constitucional va avalar el model lingüístic del sistema educatiu, però va anullar deu articles de la Llei d’educació del 2009 La impossibilitat de tenir traducció simultània durant el judici del procés independentista va generar diverses mostres de rebuig , en un any en què les sentències en català van arribar a ser només d’un 7,7% En aquest sentit, el Consell d’Europa també va demanar a l’Estat espanyol que assegurés la…
deltoide
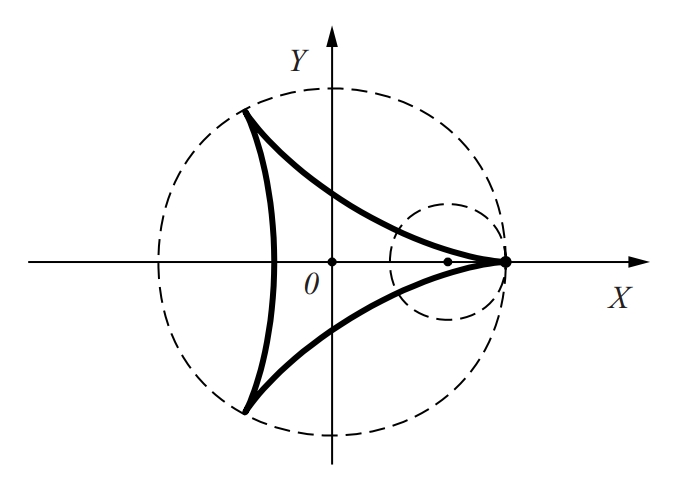
deltoide
Matemàtiques
Hipocicloide d’un cercle de radi k que roda, sense lliscar, dintre d’un altre que té el radi triple.
Les seves equacions paramètriques són x = k 2cos t + cos 2t , i y = k 2sin t + sin 2 t
línia trigonomètrica
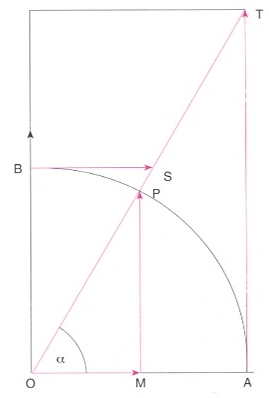
línies trigonomètriques de l’angle α (OA=1); sin α=MP; cos α=OM; tg α=AT; cotg α=BS; sec α=OT; cosec α=OS
© Fototeca.cat
Matemàtiques
Cadascun dels segments amb els quals hom representa geomètricament, basant-se en una circumferència de radi 1 (cercle goniomètric), les funcions trigonomètriques.
amplitud
Física
Valor màxim que pren una magnitud vibratòria o oscil·lant en un semiperíode.
Quan la magnitud vibratòria pot ésser expressada per una funció sinusoidal del tipus ft = A sin οt + ϕ, l’amplitud val A i correspon al cas en què sin οt + ϕ val 1
Joan Chabàs i Martí
Literatura
Novel·lista, poeta i crític, estudià dret i lletres a Madrid.
Exiliat a Cuba després de la guerra civil de 1936-39, fou professor de literatura a Santiago Escriví, en castellà, poesia Espejos, 1920, novella Sin velas, desvelada , 1927 Puerto de sombra , 1928 Agor sin fin , 1930 i la biografia Juan Maragall, poeta y ciudadano 1935 Són especialment importants la seva Historia de la literatura española 1932 i, sobretot, Literatura española contemporánea 1952
fórmula de Clairaut
Física
Fórmula que dóna el valor de l’acceleració de la gravetat g en un punt de latitud φ.
L’expressió teòrica és g = g e 1 + 5ω 2 a /2 g e - e sin 2 φ, on g e és el valor de la gravetat a l’equador, a és el semieix major equatorial de l’ellipsoide de referència, e és la seva ellipticitat i w és la velocitat angular de la Terra El valor numèric és donat per l’expressió g = 978,049 1-0,0052884 sin 2 φ, on hom ha pres com a ellipsoide de referència un d’aplatament 1/297
tangent d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i una circumferència de radi unitat centrada en el punt d’intersecció dels eixos (cercle goniomètric), i un segment que forma un angle α amb l’eix d’abcisses x, longitud del segment, perpendicular a l’eix d’abcisses, deteminat entre el punt de la circumferència de coordenades (1,0) i el punt en què aquest segment s’interseca amb el segment inclinat l’angle α en qüestió.
Aquesta longitud és la tangent de l’angle α, i és denotada per tgα És vàlida la següent igualtat tgα=sin α/cos α, on sin és el sinus d’un angle i cos és el cosinus d’un angle La tangent de l’angle α determinat entre dos segments qualssevol és la tangent de l’angle que, dibuixat sobre el cercle goniomètric, té la mateixa obertura que α Algunes fòrmules trigonomètriques relatives a la tangent d’un angle són tgα+β=tgα+tgβ/1-tgα- tgβ tg-α=-tgα tgα+tgβ- =sinα+β/cosα cosβ
sinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i un segment de longitud unitat OP que forma un angle α amb l’eix d’abscisses x, valor de la projecció de OP sobre l’eix y
.
Aquesta projecció és el sinus de l’angle α i és denotada per sinα El sinus de l’angle α determinat entre dos segments qualssevol és el sinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al sinus d’un angle són sinα+β = sinα cosβ - cosα sinβ sin-α = -sinα sinα sinβ = cosα-β - cosα+β/2 sinα + sinβ = 2 sinα+β/2 cosα-β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α+sin 2 α=1
producte vectorial de dos vectors
Matemàtiques
Operació definida entre dos vectors.
Donats dos vectors, a i b , vector a ∧ b el mòdul del qual és | a ∧ b | = | a | | b | sin a , b , on sin a , b és el sinus de l’angle que determinen les direccions de a b , i la direcció del qual és perpendicular al pla determinat per a i b , i el sentit del qual és tal que el tríedre a , b , a ∧ b sigui dextrogir és a dir, que el sentit de a ∧ b és igual al sentit d’avanç d’un llevataps que, aplicat en el punt de concurrència de a i b , anés del primer cap al segon