Resultats de la cerca
Es mostren 505 resultats
perfil
Transports
Secció d’una ala, del caire d’atac al caire de sortida, paral·lelament al pla de simetria.
Geomètricament és caracteritzat pel fet de tenir el caire de sortida en punxa, forma essencial per a produir la sustentació La corda del perfil, que és la línia de referència dels angles d’atac, pot ésser definida com la recta que uneix el caire de sortida del perfil amb el centre de la circumferència que té quatre punts de contacte amb el caire d’atac del perfil La línia mitjana és el lloc geomètric dels centres de les circumferències tangents als contorns del perfil Hom anomena curvatura del perfil la distància màxima de la línia mitjana a la corda El gruix del perfil és donat pel major…
agrimensura
Geografia
Part de la topografia que tracta de la determinació de les superfícies agràries i de les particions dels terrenys.
La mesura i el repartiment de les terres foren les primeres qüestions de caràcter geomètric que, en néixer l’agricultura, preocuparen la humanitat Els primers testimonis de l’agrimensura es troben en papirs egipcis de fa uns 1700 anys aC, reproducció d’altres encara més antics L’actual tècnica de l’agrimensura consisteix a dividir el terreny en parcelles d’àrea fàcilment mesurable, cosa que hom fa, sempre que el terreny ho permet, per mitjà de triangulacions triangulació i, quan les circumstàncies no són tan favorables, per poligonacions poligonació Sobre el mateix terreny, sobretot per mitjà…
Carles Simó i Torres

Carles Simó i Torres
© Universitat de Barcelona
Matemàtiques
Matemàtic.
Llicenciat en enginyeria industrial per la Universitat Politècnica de Catalunya i en matemàtiques per la Universitat de Barcelona, on es doctorà l’any 1974, des del 1975 és catedràtic de matemàtica aplicada i anàlisi de la UB Autor de més de 200 articles, ha estudiat les propietats generals dels sistemes dinàmics, els sistemes hamiltonians i dissipatius, la mecànica celeste, l'astrodinàmica i l'anàlisi numèrica, l’anàlisi i el disseny d’òrbites de ginys espacials i els sistemes dinàmics assistits per ordinador Ha combinat mètodes diversos analític, geomètric, algèbric, numèric, etc per a l’…
Gaston Bachelard
Filosofia
Història
Filòsof francès.
Professor d’història i de filosofia de les ciències a Dijon i després a la Sorbona, es dedicà sobretot a l’epistemologia, a la filosofia de les ciències i a la psicoanàlisi en general El reconeixement de la complexitat de les teories científiques l’obligà a refusar les simplificacions introduïdes per les interpretacions racionalistes Afirmà l’existència d’un nou esperit científic, que s’oposa tant al predomini antic i medieval de la imatge com a l’esquema geomètric modern, i realitzà l’intent d’eixamplar el marc i l’estructura de la raó Enfront de la pretensió de sabers absoluts, Bachelard…
Joan Claret i Corominas
Pintura
Pintor.
Llicenciat en lletres el 1957, un any després estudia filosofia a la Universitat de Sorbona de Paris La seva formació fou bàsicament autodidàctica i el 1959 es vinculà amb la sala Gaspar, on formà part de l'activitat "Homenatge a Velázquez", organitzada pel crític d'art Santos Torroella i portada a la Biennal de Venècia Conreà una pintura sota una concepció d’espais i formes oberts, resolta amb la composició, el ritme i l’organització controlada Creà, així, un expressionisme molt personal de tipus geomètric i, en general, abstracte, en què dominen el blanc, el negre i el gris Exposà…
László Moholy-Nagy
Pintura
Fotografia
Pintor, fotògraf i teòric de l’art hongarès.
Anà a Berlín el 1920, on assimilà les obres dels dadaistes i dels constructivistes holandesos Hi exposà a la galeria Der Sturm 1922, i, invitat per WGropius com a professor al Bauhaus 1923-28, proclamà la seva teoria del dinamisme universal per damunt de l’estàtica clàssica, teoria que recollí en el llibre Von Material zu Architektur ‘Del material a l’arquitectura’, 1929 i que aplicà en la creació d’escultures cinètiques de les quals fou un capdavanter i lumíniques que projecten imatges, formes i colors En 1928-33 treballà de nou a Berlín, des d’on passà a Anglaterra El 1937 s’installà a…
teoremes de Guldin
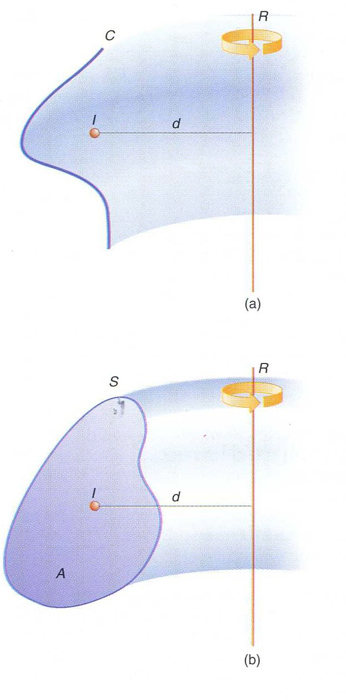
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A , que gira al…
pla
Superfície d’un cos més o menys acostada, per la seva configuració, a un pla geomètric.
guilloixat
Tecnologia
Acabat d’una superfície, fet a màquina, en forma de dibuix geomètric que es va repetint.
Long Range Aid to Navigation
Aeronàutica
Sistema de radionavegació desenvolupat durant la Segona Guerra Mundial per les forces dels EUA.
Hom obté la situació mitjançant la recepció de senyals radioelèctrics d’alta freqüència emesos per dues estacions terrestres de situació coneguda La mesura de la diferència dels temps que triguen a arribar a la nau els senyals de cada estació determina una línia de posició que és el lloc geomètric de tots els punts la diferència de distàncies a les estacions emissores dels quals és constant i igual a la trobada Tal línia de posició és una hipèrbole els focus de la qual són les estacions emissores Una altra estació determina una nova línia de posició, la intersecció de la qual amb la primera…
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- …
- Pàgina següent
- Última pàgina