Resultats de la cerca
Es mostren 278 resultats
Sofja Kovalevskaja

Sofja Kovalevskaja
Matemàtiques
Matemàtica russa.
Deixebla de Weierstrass i dotada d’un gran talent, es dedicà sobretot a l’anàlisi matemàtica, on féu notables aportacions a l’estudi de les equacions en derivades parcials i mostrà com la teoria de funcions pot ésser aplicada a problemes de física Escriví també algunes novelles
Aleksandr Mikhajlovič Ljapunov
Matemàtiques
Matemàtic i enginyer rus.
Professor a Kharkiv i a Peterburg, féu importants estudis matemàtics sobre les equacions diferencials, el càlcul de probabilitats, etc i mecànics sobre sistemes en equilibri o en moviment, sobre hidrodinàmica, potencials, etc Desenvolupà especialment una teoria general de l’estabilitat i de la regulació de sistemes no lineals
equació integral
Matemàtiques
Equació on la funció que cal determinar es troba dins l’integrant d’una certa integral coneguda.
L’exemple més simple és l’equació , on la funció f x és coneguda i cal trobar la funció f x En virtut del teorema fonamental del càlcul, la solució és, en certes condicions de regularitat, Aquestes equacions les trobem en la resolució matemàtica de problemes físics i tècnics
Herbert Western Turnbull
Matemàtiques
Matemàtic britànic.
Professor de diversos collegis i de les universitats de Liverpool 1910, de Hong Kong 1912 i d’Hostel 1913-1915, féu importants aportacions a l’estudi dels invariants i de les equacions quadràtiques Escriví The Theory of Determinants, Matrices and Invariants 1960, Introduction to the Theory of Canonical Matrices 1961, etc
René Baire
Matemàtiques
Matemàtic francès, deixeble de Tannery a l’École Normale, i després, de Volterra i Dini, a Itàlia.
Estudiant la convergència de les sèries funcionals descobrí les funcions que porten el seu nom Investigà també sobre equacions en derivades parcials Entre el 1905 i el 1914 fou professor d’anàlisi a Dijon Amb Poincaré, Borel i Lebesgue, és considerat un dels fundadors de l’actual anàlisi de variable real
principi de Hamilton
Física
Una de les formes d’enunciar el principi de la mínima acció.
L' acció elemental és definida a partir del lagrangià, dA = L dt , i el principi afirma que el moviment del sistema entre dos instants t 1 i t 2 és tal que l’acció és un extremal, és a dir, un màxim o un mínim Hom en dedueix les equacions de Lagrange
Enrico Betti
Física
Matemàtiques
Físic i matemàtic italià.
Estudià a la Universitat de Pisa, on fou director de la Scuola Normale Superiore Fou un dels primers a interessar-se per la teoria de les equacions algèbriques d’Évariste Galois Creà els nombres emprats en triangulació, que porten el seu nom, i treballà també en topologia, teoria del potencial i elasticitat
Stephen Smale
Matemàtiques
Matemàtic nord-americà.
Professor a les universitats de Princeton i Berkeley, ha fet investigacions en topologia diferencial, anàlisi global i equacions diferencials quantitatives reeixí a provar la conjectura de Poincaré per a dimensions majors que quatre, i provà que hom pot girar una esfera a l’inrevés El 1966 li fou atorgada la medalla Fields
cicloide
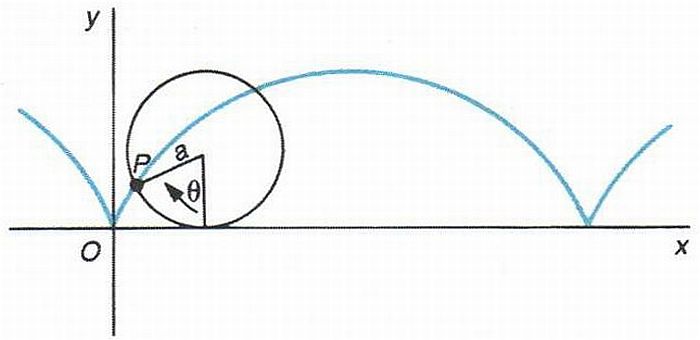
Cicloide
©
Matemàtiques
Corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una recta.
Les seves equacions paramètriques són x = a θ - sinθ, y = a 1 - cosθ Hom pot ampliar aquesta definició considerant una trajectòria fixa en lloc d’una recta així, per exemple, l' epicicloide és la corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una altra circumferència i exteriorment a ella
espiral
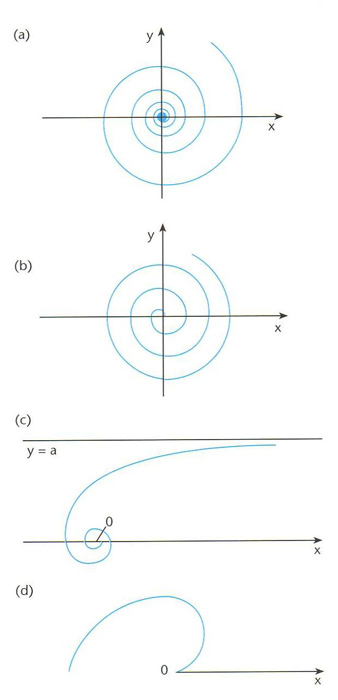
espiral: (a) logarítmica; (b) d’Arquímedes; (c) hiperbòlica; (d) parabòlica
© fototeca.cat
Matemàtiques
Corba plana descrita per un punt que gira al voltant d’un punt fix allunyant-se contínuament segons una llei determinada, característica per a cada tipus d’espiral.
Analíticament són representades gairebé sempre en coordenades polars Les equacions de les espirals més importants són espiral logarítmica o equiangular, r = e aθ espiral d’Arquimedes , r = r o /2πθ espiral hiperbòlica, r θ = a /θ espiral parabòlica o de Fermat, r 2 = a θ, i espiral sinusoidal, r n = a n sin n θ
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- …
- Pàgina següent
- Última pàgina