Resultats de la cerca
Es mostren 1178 resultats
enèsim | enèsima
Matemàtiques
Dit d’una potència, arrel, ordre de derivació, etc, indeterminats.
dialtea
Farmàcia
Ungüent emprat antigament i compost principalment d’arrel de malví.
carbassina
Botànica
Planta herbàcia vivaç, de la família de les cucurbitàcies, dioica, de tija ramificada des de la base i enfiladissa gràcies a circells oposats a les fulles palmatilobades, de flors verdoses, les mascles disposades en cimes corimboses i les femelles en umbel·les més o menys sèssils, i de baies globulars, fètides, de color vermell un cop madures.
Viu en bardisses i a les clarianes del bosc de ribera d’Europa, de l’Àfrica septentrional i de l’Àsia occidental L’arrel és un purgant dràstic
Rodrigo Paganino
Literatura
Narrador portuguès.
Els seus Contos do tio Joaquim 1861, impregnats d’una malenconia sentenciosa d’arrel popular, són una de les obres més llegides de la literatura portuguesa del s XIX
camí de dades
Electrònica i informàtica
Descripció de la ruta que s’ha de seguir a través d’una estructura de directoris per a arribar a les dades.
El camí absolut és la ruta a partir d’un punt prefixat de l’estructura de directoris directori arrel el camí relatiu descriu la ruta a partir del directori actual
polirrize | polirriza
Lingüística i sociolingüística
Dit del verb que forma els seus temps a partir d’uns temes que procedeixen d’arrels diverses (com en llatí fero/tuli/latum, o en català vaig/aniré).
Són anomenats també polirrizes els verbs que, formant els temps a partir de temes que procedeixen d’una mateixa arrel, apareixen, però, diferenciats, a causa de les transformacions fonètiques que experimenten
genciana
Botànica
Gènere de plantes herbàcies, de la família de les gencianàcies, de fulles enteres i generalment ovals, de flors poc o molt campanulades i freqüentment blaves i de fruits capsulars.
La genciana groga G lutea és força alta i té les flors grogues, es fa als Pirineus i l’arrel és emprada per les seves propietats aperitives, amargants, tòniques i estomacals
arbre
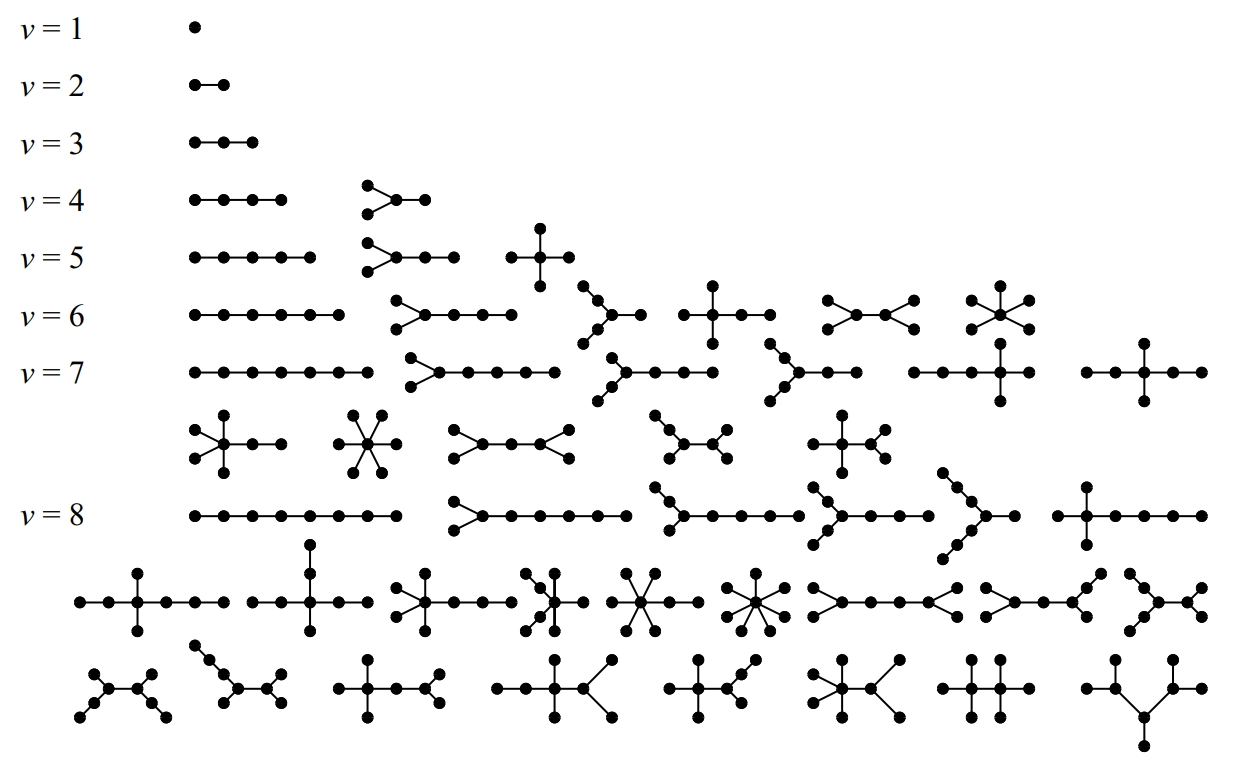
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la…
símbol
Matemàtiques
Lletra o signe gràfic de qualsevol mena utilitzat per a representar quantitats (nombres), relacions o operacions.
Cal distingir sempre el símbol del concepte Així, el nombre dos concepte pot ésser representat per símbols diferents 2, II, ╫, etc Principals símbols símbols emprats en teoria de conjunts ∈ pertany a ∉ no pertany a = igual a ≠ diferent ⊂ inclusió, és inclòs en ⊄ no és inclòs en ⋂ intersecció ⋃ reunió − diferència ∁ , − , ∽ complementari ∆ diferència simètrica → aplicació, funció ≃ coordinable, bijectiu x producte cartesià {} singletons claudàtors ∅ conjunt buit ℕ nombres naturals ℤ nombres enters ℚ nombres racionals ℝ nombres reals ℂ nombres complexos símbols emprats en lògica…