Resultats de la cerca
Es mostren 29 resultats
mètode dels elements finits
Construcció i obres públiques
Mètode de càlcul numèric que s’empra en la resolució d’equacions diferencials, basat en la discretització del medi o de l’objecte en estudi en una malla d’elements connectats en nodes.
És un mètode d’ús molt versàtil i vàlid per a una gran varietat de problemes i tipologies d’estructures Dóna lloc a un sistema lineal d’equacions que permet trobar una solució aproximada al problema
mètode dels elements finits
Matemàtiques
Mètode numèric per a resoldre problemes d’equacions diferencials en derivades parcials.
Matemàticament és una extensió de la tècnica de Rayleigh-Ritz-Galerkin el problema es planteja en forma variacional i hom aproxima la solució mitjançant una combinació lineal de funcions senzilles, en aquest cas funcions polinòmiques a trossos, nulles excepte en un petit domini dintre del qual són polinomis de grau baix El mètode aparegué els anys seixanta entorn de l’aplicació dels ordinadors als càlculs elàstics d’estructures, superà molt de pressa els mètodes de diferències finites i amplià ràpidament el seu camp d’aplicacions i es mostrà molt potent especialment quan la geometria del…
teorema dels increments finits
Matemàtiques
Teorema segons els qual si f(x) és una funció contínua en [a,b] i derivable en (a,b), aleshores existeix almenys un punt c ∈(a,b) tal que .
També és anomenat teorema del valor mitjà
Classificació dels grups finits simples (D. Gorenstein i M. Aschbacher)
Classificació dels grups finits simples D Gorenstein i M Aschbacher
Resolució de les conjectures de Weil en cossos finits (P. R. Deligne); grups de Lie (G.A. Margulis); topologia (S. Novikov); K-teoria (D.G. Quillen); anàlisi complexa multidimensional (C.L. Fefferman)
Resolució de les conjectures de Weil en cossos finits P R Deligne grups de Lie GA Margulis topologia S Novikov K-teoria DG Quillen anàlisi complexa multidimensional CL Fefferman
autòmat finit indeterminista
autòmat finit indeterminista
Matemàtiques
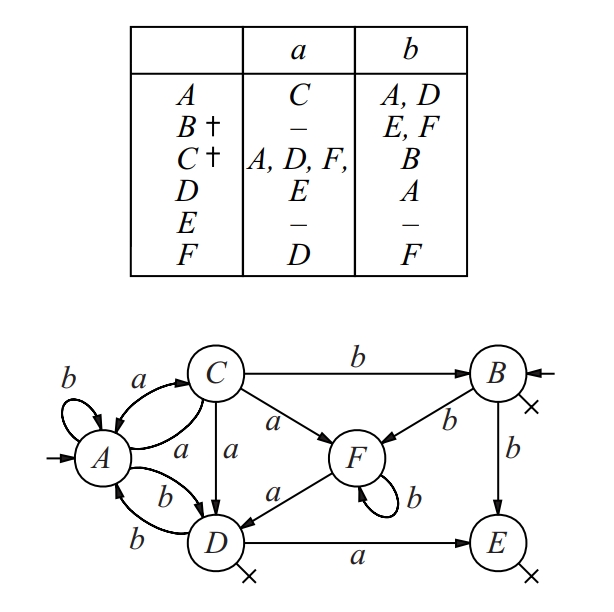
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
mode finit
Gramàtica
Mode on és expressada la categoria de persona gramatical; s’oposa a mode infinit.
En català són modes finits l’indicatiu, el subjuntiu, l’imperatiu i el condicional
John G. Thompson
Matemàtiques
Matemàtic nord-americà.
Féu contribucions importants per a la classificació dels grups finits, en demostrar que tot grup finit simple no cíclic conté un nombre parell d’elements Medalla Fields 1970 i premi Abel 2008
paral·lelisme psicofísic
Filosofia
Doctrina que, tot negant tota interrelació causal entre matèria i esperit, afirma alhora la independència i coincidència dels fenòmens propis de la realitat física i dels que pertanyen a l’àmbit psíquic.
Modalitats diferents d’aquesta doctrina són l’ocasionalisme de Malebranche, la teoria spinoziana que l’extensió i el pensament són dos modes finits de l’única substància existent, la infinita, i l’harmonia preestablerta de Leibniz
cardinal
Matemàtiques
Referit a un conjunt, classe dels conjunts equipotents al conjunt, és a dir, classe dels conjunts amb els quals el conjunt en qüestió pot establir una aplicació bijectiva.
El cardinal d’un conjunt finit és el nombre dels seus elements els cardinals dels conjunts finits formen el conjunt dels nombres naturals, ℕ La collecció de tots els cardinals no és un conjunt antinòmia de Cantor El cardinal d’un conjunt C és notat per card C o per # C