Resultats de la cerca
Es mostren 6 resultats
triangle òrtic
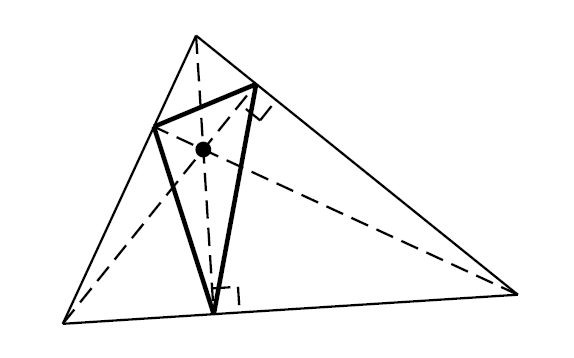
Triangle òrtic
Matemàtiques
Donat un triangle qualsevol, triangle inscrit que té per vèrtexs els tres peus de les altures del triangle donat.
L’ortocentre d’un triangle és l’incentre del seu triangle òrtic
altura
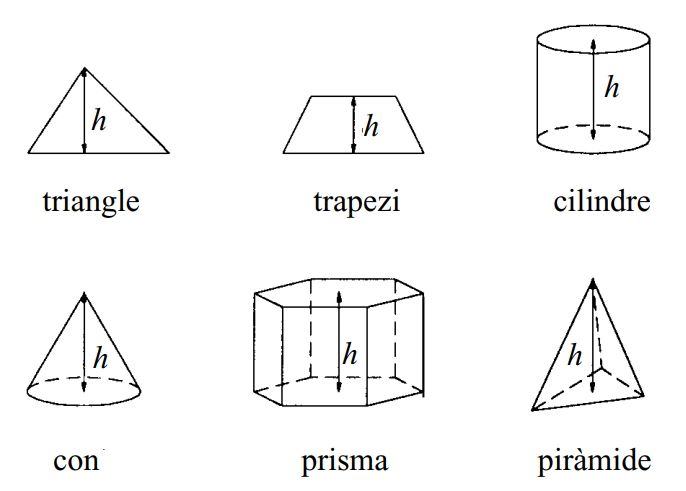
Altures de diferents figures i cossos geomètrics
© Fototeca.cat
Matemàtiques
Segment de recta (o també la seva longitud) en les figures i en els cossos geomètrics comprès entre dos de llurs elements (un vèrtex i un costat al triangle, dos costats al paral·lelogram) i perpendicular almenys a un d’aquests elements, anomenat base, o bé a una recta o a un pla que els determini.
Moltes figures i molts cossos presenten diverses altures segons quin costat hom prengui com a base En un triangle, les tres altures es tallen en un punt dit ortocentre i els seus peus determinen el triangle òrtic
triangle
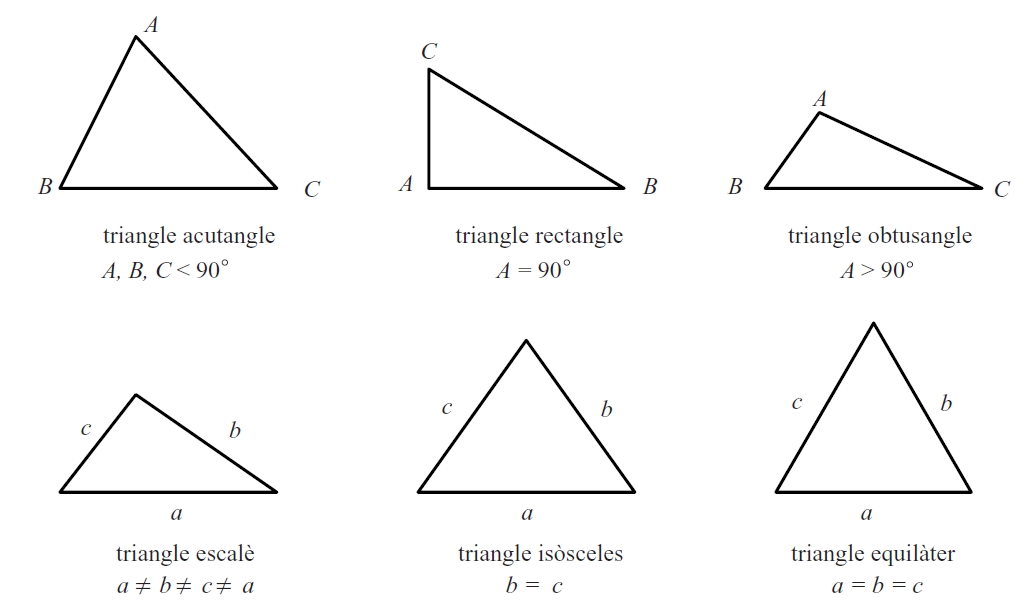
triangles
Matemàtiques
Figura formada en unir tres punts (anomenats vèrtexs) no alineats amb tres segments de línia recta.
Un triangle és anomenat acutangle si els seus angles interiors són aguts, obtusangle si té un angle interior obtús, escalè si cap costat és igual als altres dos, isòsceles si té dos costats iguals, equilàter si té tots tres costats iguals, i rectangle si un dels angles interiors és un angle recte 90° Si no és rectangle és anomenat obliquangle L’àrea d’un triangle és igual a la meitat del producte de la base qualsevol costat per l’altura recta perpendicular des del vèrtex oposat a la base fins a aquesta base La resolució d’un triangle , és a dir, la determinació dels seus angles…
teorema de la recta d’Euler
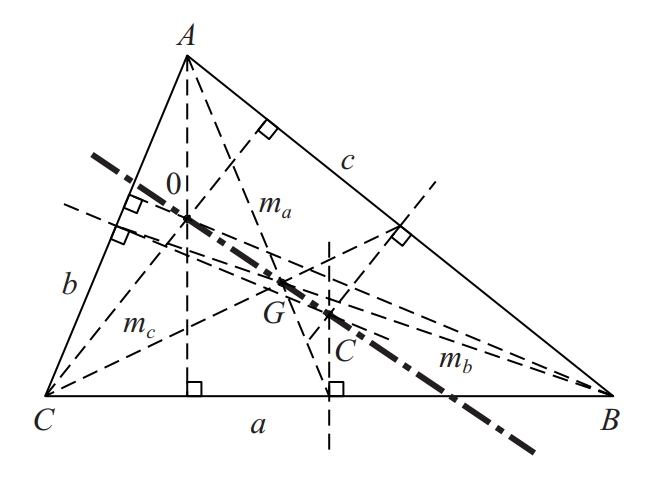
teorema de la recta d’Euler
Matemàtiques
Resultat que prova que l’ortocentre, el circumcentre i el baricentre d’un triangle estan alineats i que el baricentre és a una distància doble de l’ortocentre que del circumcentre.
La recta que passa per aquests punts s’anomena recta d’Euler
teorema de la circumferència dels nou punts
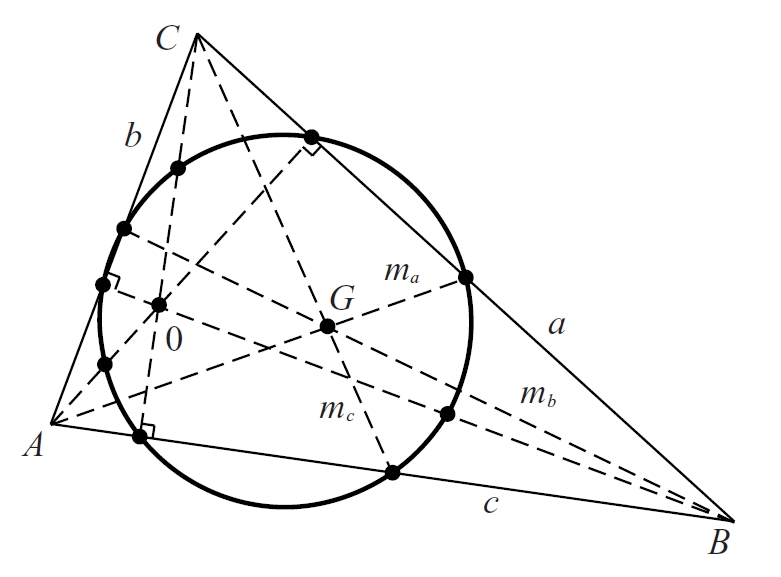
Teorema de la circumferència dels nou punts
Matemàtiques
Propietat segons la qual els peus de les altures, els peus de les mitjanes i els tres punts mitjans dels segments que van de l’ortocentre als vèrtexs del triangle són en una circumferència, anomenada circumferència dels nou punts.