Resultats de la cerca
Es mostren 25 resultats
llei de Haüy
Mineralogia i petrografia
Llei, anomenada també fonamental o dels índexs racionals.
Segons la qual si hom pren com a eixos coordenats les interseccions de tres cares d’un cristall que es tallin en un vèrtex, els quocients dels paràmetres sobre un mateix eix de totes les cares del cristall són nombres racionals quasi sempre molt simples
proporció
Matemàtiques
Igualtat de dues raons, fraccions o quocients.
En la proporció a / b = c/d , a i d són dits extrems i b i c , mitjans A partir de la proporció a / b = c/d hom pot derivar altres proporcions a+b / b = c+d / d addició, a + b / a - b = c + d / c-d si a ≠ b addició i subtracció, a/c = b/d alternació, b/a = d/c si a =0 inversió, i a-b / b = c-d / d subtracció
coeficient
Física
Magnitud que caracteritza una determinada propietat d’un sistema.
Generalment, és expressada per un quocient o un producte de magnituds de diferents espècies, de manera que el seu valor numèric té dimensions i ha d’expressar-se en termes d’una unitat de mesura, la qual prové del quocient o del producte de les unitats de les magnituds que el defineixen Hom no ha respectat sempre aquesta definició estricta i sovint ha confós els coeficients amb els factors , els quals són normalment quocients de magnituds de la mateixa espècie i, per tant, són nombres adimensionals
fracció contínua
Matemàtiques
Expressió de la forma
on l’algorisme s’estén indefinidament.
Hom l’expressa abreujadament mitjançant la notació a 0 + a 1 / b 1 + a 2 / b 2 + a 3 / b 3 + Són emprades per a representar nombres irracionals Així, si α 0 és un nombre irracional positiu, i n ≥0, α 0 admet l’expressió on u n és la part entera de α i α n ≥1 és definit per la relació de recurrència α n - 1 = u n - 1 + 1/α n , n≥1 La successió u n n ≥ 0 és el desenvolupament de α 0 en fracció contínua , i els coeficients u n són els quocients incomplets de la fracció contínua Un exemple d’aquest tipus de desenvolupament és el del nombre π/4, fet per William Brouncker
sistema d’Hondt
Política
Dret
Variant del sistema de càlcul electoral dit de representació proporcional aproximada que amb una sola operació permet d’obtenir un primer repartiment d’escons a base del quocient i un altre repartiment que té en compte la mitjana més forta.
Al moment de repartir els escons, en nombre n , entre els candidats de les diverses llistes sotmeses a votació, el nombre de vots assolits per cadascuna d’elles són dividits successivament per 1, 2, etc fins a n A continuació són ordenats, del més alt al més baix, els quocients obtinguts i el que ocupa el lloc n és el “quocient aproximat” o “divisor electoral” Talment com indica el seu nom, aquest “quocient” és emprat tot seguit com a “divisor” del nombre de vots de cadascuna de les llistes, operació que dóna com a resultat el repartiment d’escons segons la mitjana més forta El…
anàlisi foliar
Agronomia
Anàlisi dels teixits vegetals amb l’objectiu de determinar l’estat nutritiu d’un cultiu.
Per obtenir una correcta interpretació de l’estat nutritiu del cultiu és important definir el teixit a analitzar i en quin moment fer-ho ja que la concentració de nutrients és variable segons la seva funció, posició en la planta, edat i estadi de maduració Les fulles o els pecíols foliars són sovint els teixits escollits La interpretació de la concentració de nutrients es pot fer utilitzant valors de concentracions individuals, amb l’inconvenient que no es té en compte l’efecte de possibles interaccions entre elements en l’estat nutritiu del cultiu, o bé utilitzant quocients…
número d’or
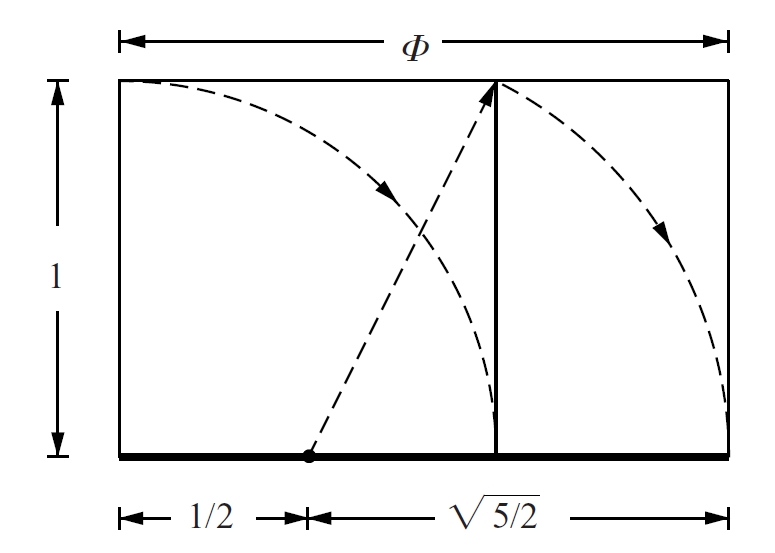
número d’or
Matemàtiques
Nombre irracional algebraic positiu que, elevat al quadrat, és igual a ell mateix més una unitat: (1 + ⎷5 ) ⁄ 2 = 1,618.
El número d’or apareix en molts problemes geomètrics relatius a les divisions harmòniques de segments o a proporcions de rectangles, o entre mides Així, un rectangle té de proporció el número d’or si, i solament si, té la mateixa proporció del rectangle que resulta de treure del rectangle original un quadrat Aquest nombre és el límit dels quocients 1 ⁄ 1, 2 ⁄ 1, 3 ⁄ 2, 5 ⁄ 3 dels termes de la successió de Fibonacci i té una important presència en elements naturals i artístics, especialment en pintura i arquitectura, ja que que el número d’or és igual al cosinus de 36º i, per tant…
entropia
Física
Magnitud termodinàmica, funció d’estat del sistema, introduïda per Clausius.
Hom la defineix per S 2 — S 1 = ∫ 2 1 dQ/T, S 2 — S 1 essent la variació d’entropia corresponent a dos estats d’equilibri del sistema, i ∫ 2 1 dQ/T , la suma de quocients de les quantitats de calor cedides al sistema i la temperatura absoluta en què es troba el sistema en tots els punts d’un procés reversible qualsevol que uneixi l’estat 1 amb el 2 L’entropia proporciona un criteri per a determinar quins són l’estat inicial i el final d’una evolució termodinàmica, puix que en qualsevol procés d’un sistema aïllat l’entropia augmenta o roman constant segon principi de la…
numerador
Matemàtiques
En general, expressió numèrica o literal que és escrita damunt la ratlla horitzontal que indica divisions i quocients.
secció àuria
Música
Proporció que ja es troba enunciada en el Timeu de Plató i apareix descrita en els Elements d’Euclides, el qual, en dividir un segment donat (ab) en dues parts desiguals, observà com la petita es comporta, amb relació a la més llarga, de la mateixa manera que la totalitat del segment amb relació a la primera (ac/cb = ab/ac).
El valor numèric dproporció s’expressa aritmèticament amb el número 1,618, i fou anomenada "divina proporció" pel teòleg i matemàtic Luca Pacioli en el seu tractat De divina proportione Venècia, 1509 L’expressió secció àuria nombre d’or prové de Leonardo da Vinci, que illustrà les figures geomètriques del tractat de Pacioli El nombre d’or apareix com una llei bàsica de la morfologia de la natura i constitueix la base de l’estructura figurativa del cos humà Des de l’Antiguitat fins al Renaixement els artistes i arquitectes se’n serviren per a expressar les correspondències harmòniques entre l’…