Resultats de la cerca
Es mostren 145 resultats
finit | finita
Matemàtiques
Dit d’un objecte matemàtic (nombre, figura, regió, etc) fitat, que no és infinit.
finit | finita
conjunt finit
Matemàtiques
Conjunt amb un nombre finit d’elements.
Formalment, és un conjunt equipotent a un nombre natural necessàriament únic que compta els elements del conjunt Equivalentment, un conjunt és finit quan el seu cardinal és un nombre natural
autòmat finit
Matemàtiques
Electrònica i informàtica
Model matemàtic d’un sistema que té un nombre finit d’estats d’entrada i de sortida —els quals representen les diferents configuracions de signes (i estats interns) que representen la capacitat que té el sistema d’enregistrar els esdeveniments passats— i en el qual l’estat de sortida depèn en qualsevol moment de l’entrada present i dels estats interns.
Per tant, un autòmat finit es defineix pel conjunt finit dels estats d’entrada, de sortida i interns possibles per una funció que dóna el següent estat intern corresponent a un estat d’entrada i a un estat intern donats i per una funció que determina l’estat de sortida següent Aquest concepte és essencialment abstracte i té valor tant per a descriure programes com per a descriure aparells Un autòmat finit concret es defineix normalment per mitjà de la seva taula d’estats , que consisteix en una llista de les relacions existents entre els estats d’entrada…
conjunt finit
Matemàtiques
Conjunt en el qual tota mena d’autoaplicació injectiva, definida en ell, és també bijectiva; el seu cardinal és el nombre d’elements que conté.
mode finit
Gramàtica
Mode on és expressada la categoria de persona gramatical; s’oposa a mode infinit.
En català són modes finits l’indicatiu, el subjuntiu, l’imperatiu i el condicional
autòmat finit determinista
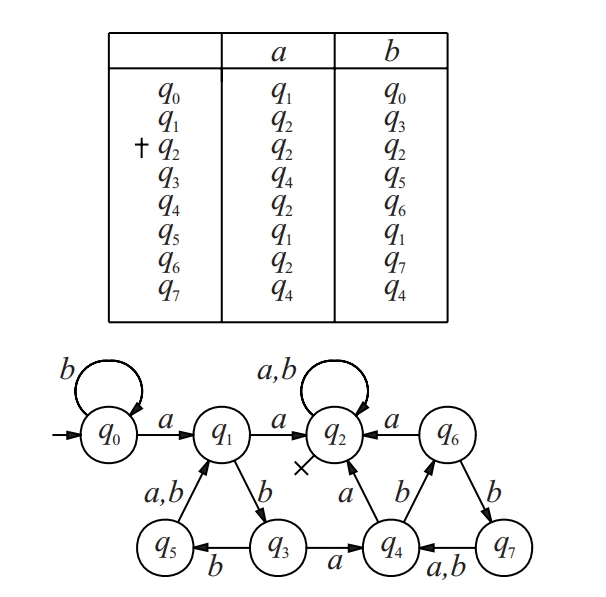
autòmat finit determinista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, q0, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet, anomenat d’entrada; δ : Q ⨉ ∑* → Q és la funció de transició que satisfà ∀q ∈ Q, ∀x,y ∈ ∑*:δ(q, λ) = q, δ(q, xy) = δ(δ(q, x), y) essent xy la concatenació de x i de y, i λ la paraula buida i ∑* el conjunt de paraules; q0 ∈Q s’anomena estat inicial; F ⊂ Q s’anomena conjunt d’estats finals o acceptadors.
Usualment un autòmat finit determinista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si δ q i , a = q j S’indica l’estat inicial amb una fletxa i els finals amb una creu
autòmat finit indeterminista
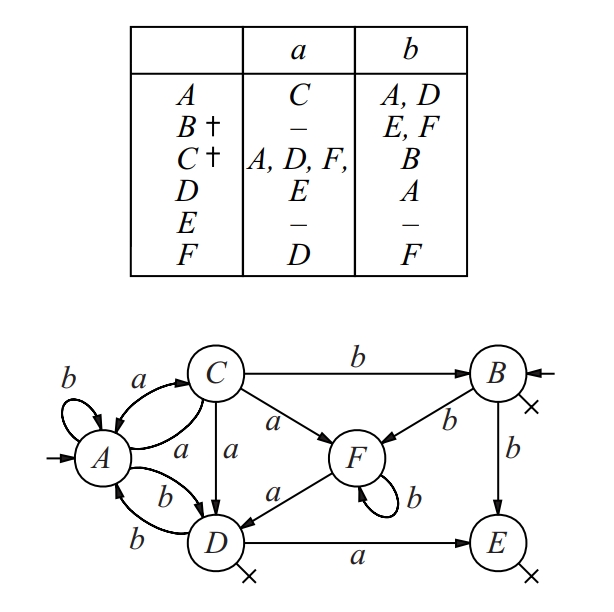
autòmat finit indeterminista
Matemàtiques
Estructura de la forma M = (Q, ∑, δ, I, F) on Q és un conjunt finit no buit, els elements del qual s’anomenen estats; ∑ és un alfabet anomenat d’entrada; δ : 2Q ⨉ ∑* → 2Q és la funció de transició que satisfà ∀P1, P2 ⊂ Q, ∀x, y∈∑*: δ(∅, x) = ∅, δ(P1, λ) = P1, δ(P1 ∪ P2, x) = δ(P1, x) ∪ δ(P2, x), δ(P1, xy) = δ(δ(P1, x)y), essent xy la concatenació de x i de y i ∑* el conjunt de paraules; I ⊂ Q és el conjunt d’estats inicial; F ⊂ Q és el conjunt d’estats finals o acceptadors.
Usualment un autòmat finit indeterminista es descriu mitjançant el seu diagrama de transicions Es tracta d’un graf dirigit que té els estats per vèrtex si un arc que va de q i a q j amb etiqueta a si q j ∈ δ q i , a S’indiquen els esstats inicials amb fletxes i els finals amb una creu Els llenguatges acceptats pels autòmats finits indeterministes són els mateixos que els reconeguts pels finits deterministes regulars L’avantatge dels indeterministes enfront dels deterministes és la facilitat de maneig i de construcció
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina