Parlem de l’infinit

En aquest article vull exposar algunes reflexions sobre l’infinit. Què és? Hi ha diferents ordres de magnituds “molt grans”? Quina és l’aritmètica de l’infinit? Comencem!

Què és l’infinit?

Per tal d’entendre el concepte d’ordre de magnitud i de grandària, proposo que el lector intenti contestar (o com a mínim reflexionar) les següents qüestions de la manera més raonada possible:

• Hi ha més números enters que fraccionaris (tenint en compte que els enters estan formats pels naturals i els seus oposats), és a dir: ....., -4, -3, -2, -1, 0, 1, 2, 3, 4, .........?
• Hi ha la mateixa quantitat de parells que senars?
  
  • En cas afirmatiu, sembla que la quantitat de números parells “dividit” entre la quantitat de números senars és 1, oi?
• Hi ha el doble d’elements en el conjunt d’enters que en el conjunt de naturals?
  
  • Si és cert, la quantitat de números enters “dividit” entre la quantitat de números naturals és 2, oi?

Penseu una mica en aquest embolic i més endavant hi donarem respostes.

El primer cop que va aparèixer el símbol de l’infinit com el coneixem avui en dia (∞, +∞ i -∞) va ser quan el matemàtic anglès John Wallis (1616-1703) va interpretar el següent quocient: .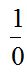

Segons Wallis, no hi ha cap número real, per gran que sigui, que multiplicat per zero doni com a resultat 1, i va anomenar aquesta expressió infinit 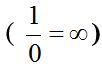, escrit amb el símbol ∞ que coneixem fins avui. Aquest símbol també es coneix com el llaç de l’amor.

Tot i això, el personatge que va liderar la descoberta dels “números infinits” va ser el matemàtic alemany George Cantor (1845-1918), que va classificar les diferents grandàries d’infinits.

Aritmètica de l’infinit: el pot dels infinits caramels

Ara aprendrem algunes operacions d’aritmètica dels infinits. Per fer-ho més senzill us proposo el següent exercici:

Imaginem un pot amb infinits caramels; ara, responeu les preguntes: si traiem un caramel quants caramels queden? I si en traiem dos?

La resposta a les dues preguntes és “infinits caramels”. Per això podem determinar  que, en general, si d’infinit traiem una quantitat positiva, p, el resultat que sempre quedarà és infinit. És a dir:

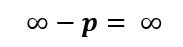
Anteriorment us he plantejat unes preguntes que us recordo:

Hi ha la mateixa quantitat de parells que senars? En cas afirmatiu sembla que la quantitat de números parells “dividit” entre la quantitat de números senars és 1, oi? Hi ha el doble d’elements al conjunt de naturals que al conjunt de parells?

Si ho rumien una mica obtenim que

De fet, tenim quocients de la forma 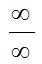 que prenen valors diferents:

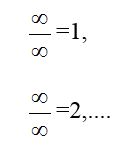
És sorprenent, hi ha resultats diferents!!!

En les dues operacions, doncs, estem davant d’una situació del tipus 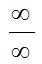, els casos anteriors ens diuen que hi ha diferents grandàries d’infinit; els de grandària més petita es diuen àlef subzero i se simbolitza així: 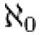(àlef és la primera lletra de l'alfabet hebreu).

Per tant, és obvi que el quocient de la forma 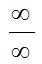 no sempre té el mateix valor, sinó que depèn de la grandària de l’infinit, per això s’anomena forma indeterminada o indeterminació.

Els casos d’indeterminacions es redueixen a set, que són els següents:     

En combinar nombres (diguem-li “a”) amb infinits i infinits entre infinits s’obtenen les següents relacions aritmètiques:

La paradoxa de l’infinit: l’hotel de Hilbert, un allotjament per a infinits comensals

David Hilbert

La paradoxa de Hilbert de l’hotel infinit és una faula inventada pel matemàtic alemany David Hilbert (1862-1943), per tal d'il·lustrar les aparents contradiccions que apareixen en tractar amb conjunts infinits.       

Tot seguit us l’explico una mica adaptada per mi.

L’hotel infinit és un hotel amb tantes habitacions com números naturals hi ha, és a dir, infinits, i estan degudament numerades (1, 2, 3, 4, 5…). Ara imaginem que totes les cambres estan ocupades i que una nit d’hivern un viatger truca a les portes de l’hotel. La recepcionista, a qui els recursos no li manquen, malgrat gaudir de plena ocupació, es va empescar la manera de col·locar el nouvingut: va fer passar cada hoste a l’habitació següent a la que tenia assignada, i va situar l’últim viatger que havia arribat a la cambra número 1. Per descomptat, l’hàbil maniobra que va fer la recepcionista per a un viatger solitari la podria fer per a 2 i per a 225.405, per exemple.

Però la cosa es va posar més interessant a l’hotel. Després d’haver resolt satisfactòriament l’allotjament per al darrer hoste, a l’hotel va arribar un autocar carregat d’infinits turistes. La recepcionista tampoc es va amoïnar gens ni mica: va fer traslladar els hostes a les habitacions que tenen el doble del número de les que actualment ocupen (el de l'1 passa a la 2, el de la 2 a la 4, el de la 3 a la 6…). Així, li van quedar lliures totes les habitacions senars i allí hi va anar allotjant els membres del grup per ordre estricte de baixada de l’autocar.

Sense reserva prèvia, la nit següent van arribar infinits autocars a l’hotel, tots ells amb infinits passatgers, i tots volien dormir a l’hotel. Encara que la solució sembli impossible, la recepcionista la va acabar trobant.

Ara que heu llegit aquesta petita sinopsi us convido a visualitzar el vídeo que us acabarà d’aclarir la paradoxa amb imatges.

Amb tot plegat, la paradoxa de Hilbert ens confirma que:

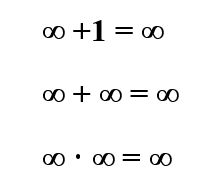
Rareses de l’infinit!

Nota: Foto de capçalera, Gerd Altmann