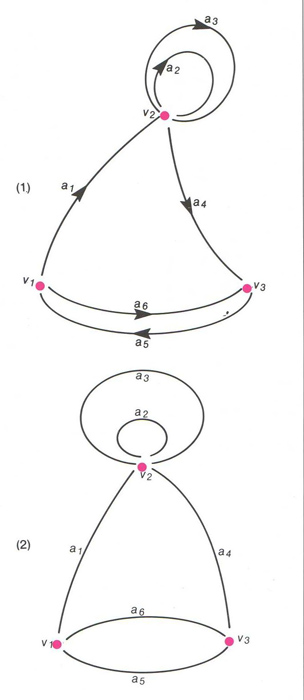
Cal distingir entre un graf orientat i un graf no orientat. Un graf orientat és una quaterna ( S, C, o, e ), on S és el conjunt d’elements o vèrtexs, C és el conjunt de línies (entre els vèrtexs) o arcs, o és l' aplicació origen (que assigna a cada arc el vèrtex del qual surt), i e és l' aplicació extrem (que assigna a cada arc el vèrtex al qual arriba). Un graf no orientat és una terna ( S, C, e ), on S és el conjunt dels vèrtexs, C és el conjunt de línies (entre els vèrtexs) o arestes , i e és l’aplicació que assigna a cada aresta una parella de S × S , formada pels vèrtexs que uneix l’aresta en qüestió. L' ordre d’un graf és el nombre de vèrtexs que el formen. En l’àrea francòfona, el terme graf és emprat sovint com a sinònim de graf orientat i graf simple o multigraf ho és de graf no orientat; en l’àrea anglòfona, el terme graf és emprat sovint com a sinònim de graf no orientat. En un graf orientat, hom parla de camins (seqüència d’arcs adjacents en què l’extrem de l’un coincideix amb l’origen del següent), de circuits (camí que comença i acaba en un mateix vèrtex), de bucles o rulls (arc que comença i acaba en un mateix vèrtex); en el cas de grafs no orientats els termes anàlegs són els de cadenes , cicles i bucles o rulls , respectivament. La teoria de grafs , originàriament lligada a la teoria de probabilitats, és considerada avui una part de la matemàtica amb entitat pròpia; permet de tractar gràficament problemes formalment complexos, i troba aplicació en nombroses branques de la matemàtica (àlgebra, combinatòria, topologia algèbrica, lògica matemàtica, etc).
m
Matemàtiques