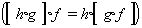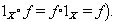categoria

per a tot parell X,Y d’objectes de la categoria existeix un conjunt Hom (X,Y), anomenat conjunt de morfismes de X en Y, tal que Hom(X,Y) = Hom(X’,Y’) si i només X=X’ i Y=Y’; i, per a tot triplet X,Y,Z d’objectes de la categoria, existeix una aplicació Hom (Y,Z) x Hom(X,Z)→Hom(X,Z), anomenada composició de morfismes, que satisfà l’associativitat

i l’existència d’una identitat a cada Hom(X,X) (és a dir, existeix un morfisme 1 _x tal que per a tot f de Hom(X,X) se satisfà Els objectes d’una categoria no han de formar necessàriament un conjunt, sino una classe; així, per exemple, la categoria dels grups ( G r ) és constituïda pels grups (objectes) i per llurs homomorfismes (morfismes) i la categoria dels espais topològics ( T op ) ho és pels espais topològics (objectes) i per llurs aplicacions contínues (morfismes). D’altres exemples són: categoria dels conjunts ( C on , conjunts i aplicacions), la dels grups abelians ( A b , grups abelians i homomorfismes), i la dels A -mòduls sobre un anell A ( M od, A -mòduls i aplicacions A -lineals). Les categories es relacionen mitjançant functors (functor).