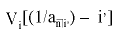Aquest sistema d’amortització és especialment aplicable en el cas que els elements patrimonials hagin estat finançats mitjançant préstecs a llarg termini o emprèstits; en aquest cas les quotes d’amortització han d’atendre no solament el reintegre del capital prestat sinó a més a més les càrregues financeres inherents. Per aquest motiu, l’amortització de préstecs i emprèstits és la segona accepció important del terme amortització financera . El fonament d’aquest tipus d’amortització és la concepció del bé patrimonial com un capital fructífer que necessita destinar part de la utilitat que produeix a la seva substitució. Els sistemes d’amortització financera són aquells que donen transcendència en l’ordre econòmic comptable de les amortitzacions al fenomen de l’interès. Hom els classifica en simples i composts. En ambdós tipus de sistemes les quotes d’amortització capitalitzades han de reconstruir el valor de l’element amortitzable, a fi que en el seu moment, mitjançant la liquidació dels valors en què les quotes d’amortització i llurs rendiments han estat materialitzats, pugui ésser finançada la substitució, renovació o reemplaçament de l’element patrimonial amortitzat. És a dir, les quotes d’amortització més llurs interessos han d’ésser concretades o materialitzades en elements patrimonials capaços de produir un rendiment. Aquest rendiment, però, pertany al concepte de l’actiu fons d’amortització i no ha d’ésser considerat mai un benefici d’explotació. La diferència entre sistemes simples i composts consisteix que els primers parteixen del principi que les quotes més llurs interessos han de reconstruir el valor inicial, mentre que els segons pretenen de reconstruir el valor final. Els sistemes més utilitzats són els composts, puix que hom considera que les quotes d’amortització més llurs rendiments capitalitzats tendeixen no a l’estricta reconstrucció del valor de l’element, sinó de l’esmentat valor més el rendiment normal que correspongui a la seva immobilització de capital. És a dir, qualsevol element patrimonial de l’empresa, i concretament els de l’actiu fix, impliquen una immobilització financera, a la qual ha d’ésser atribuït un interès. L’amortització de préstecs i emprèstits és aquella amortització financera que tracta de la reconstrucció del valor total —capital més els seus interessos— dels préstecs i emprèstits. Els tipus de préstecs, segons la forma de liquidació, es classifiquen en: préstecs amortitzables per un reembors únic (hom distingeix dins aquest cas el pagament únic que comprèn el reembors del capital conjuntament amb els interessos acumulats, o bé la liquidació del capital en un pagament únic i dels interessos en pagaments periòdics) i préstecs amortitzables mitjançant una sèrie de pagaments constitutius d’una renda , els termes de la qual comprenen els interessos del capital i una quota d’amortització destinada a l’extinció del deute. Dins aquest sistema cal notar els procediments següents: amortització per quotes fixes de capital o d’anualitat constant, sistema del fons d’amortització, sistema francès o d’amortització progressiva i sistema alemany o de pagaments d’interessos per anticipat. En el sistema d’amortització per anualitat constant , les quotes pagades seran sempre iguals, és a dir, que si anomenem a 1 , a 2 ... a n els diferents pagaments, serà a 1 = a 2 = a n . Si es tracta del sistema simple que intenta la reconstrucció del capital inicial o valor de cost, aquest serà igual a les diferents anualitats multiplicades per (1 + i) 1 , (1 + i) 2 , (1 + i) n - 2 , (1 + i) n - 1 , respectivament. És a dir, la suma dels valors actuals en cada any. La suma seria, doncs, a(1 + i) n - 1 + a(1 + i) n - 2 + ... + a(1 + i) + a = V i , essent V i el valor inicial, i el tant d’interès i n el nombre d’anys de durada del préstec. La suma de l’anterior successió dóna
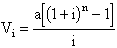
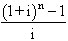
a qualsevol taula financera, hom pot trobar l’anualitat d’amortització, que té per fórmula
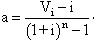
En el cas que es reconstrueixi el valor final, és a dir, que se segueixi el sistema compost, hom faria la multiplicació de les anteriors expressions per (1 + i) n . El sistema del fons d’amortització pretén d’evitar l’inconvenient que planteja el mètode anterior, que consisteix en la impossibilitat d’atendre a la llarga els dos objectius conjuntament: constància en els interessos anuals i seguretat de reconstruir el capital. L’esmentat inconvenient obeeix al fet que el tipus d’interès que pot obtenir el prestamista en les inversions complementàries que faci amb les quantitats rebudes sol ésser menor que el tipus fixat per al préstec. Aquest sistema ho evita, a través de dos tipus d’interès. El prestatari ha de satisfer una anualitat que és suma de dos conceptes: primerament, els interessos del capital al tant d’interès normal per a préstecs en el termini considerat i, segonament, la quota necessària per a reconstruir en n anys el capital, mitjançant la seva col·locació al tant per cent representat per i’ que regeix en el mercat per a les inversions complementàries. L’anualitat a pagar serà
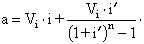
Però, per tal com les taules financeres donen el resultat d’aquesta fórmula a través d’un altre terme, pot ésser expressada l’anterior fórmula de l’anualitat de la manera següent:
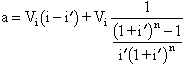
que no és més que l’expressió utilitzada abans transformada en una d’equivalent mitjançant alguns canvis propis de la matemàtica d’operacions financeres. La fracció que multiplica el capital del préstec V i en el segon membre es troba a les taules financeres com
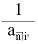
per tant l’anualitat és finalment:
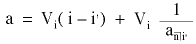
essent V i el capital inicial del préstec, i l’interès fixat pel préstec, i’ l’interès real que regeix posteriorment i n el nombre d’anys. En la pràctica les inversions complementàries al tant per cent representat per i’ poden adoptar fórmules molt diverses; totes elles englobades, però, en la denominació de fons d’amortització perquè en essència el sistema no s’altera en els seus punts bàsics, puix que la quota de reconstrucció del capital també és constant i a més igual a la fórmula