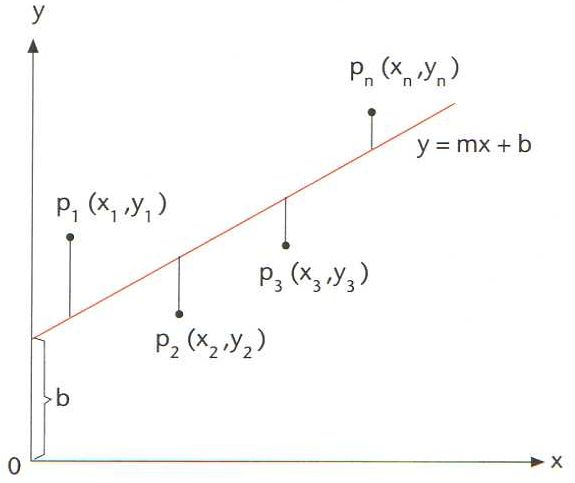
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions,
ha d’ésser mínima, entenent per desviació en un punt (xi, yi) la diferència di = yi - (mxi + b).
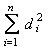
Hom pot demostrar que aquella condició condueix a les dues equacions
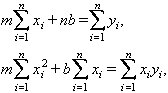
a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió. D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc., i és utilitzat en l’estudi de la correlació i en nombrosos problemes d’estadística aplicada a la ciència, a la tècnica, a l’economia, etc.