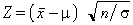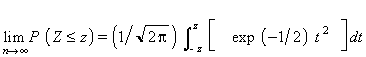Segons aquest teorema, per a n → ∞ la mitjana de n observacions independents segueix una llei normal de mitjana igual a la de la població i de variància igual a 1/n de la d’aquesta. A la pràctica, per a n ≥ 10 l’aproximació és ja suficient.
Aquest teorema, formulat per Lindeberg i Levi, és un dels més importants de la teoria de probabilitats. De Moivre en feu la primera demostració el 1732 en el cas d’una distribució binomial, i posteriorment Ljapunov en demostrà la validesa molt general en cas de variables aleatòries. Això explica per què a la pràctica hi ha moltes variables que segueixen una distribució aproximadament normal.