Resultats de la cerca
Es mostren 42 resultats
generació d’harmònics secundaris
Física
Procés òptic no lineal en què fotons d’un raig de llum interaccionen amb un medi no lineal per esdevenir fotons amb el doble de freqüència, el doble d’energia i la meitat de longitud d’ona que els fotons inicials.
La generació d’harmònics secundaris per part del collagen sota l’efecte d’un làser és utilitzada en la microscòpia òptica d’alta resolució en els camps de la medicina i la biologia Aquest efecte té el seu equivalent en radiotècnia en la duplicació realitzada per un circuit o un dispositiu multiplicador de freqüència
tub acústic
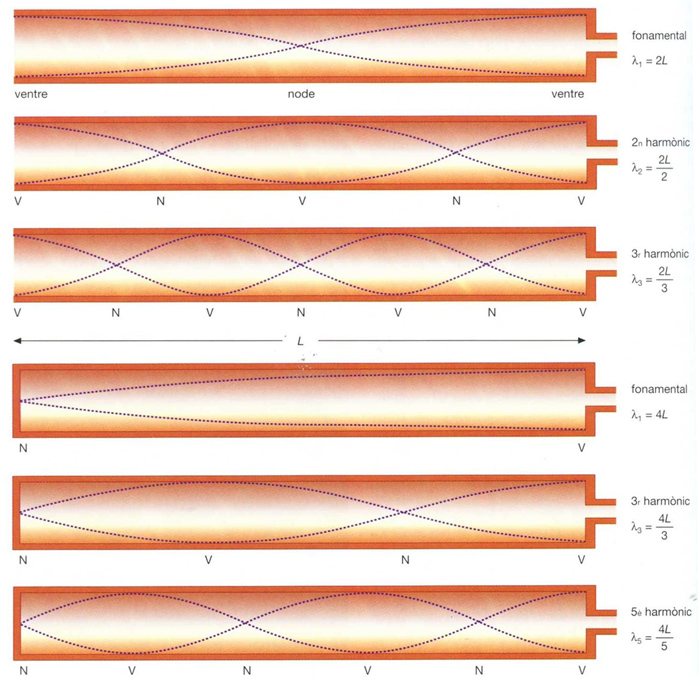
Vibracions en un tub: 1, obert (a, fonamental; b i c, harmònics); 2, tancat (a, fonamental; b i c, harmònics senars)
© Fototeca.cat
Física
Qualsevol tub de metall o de fusta, de secció quadrada, cònic o bé cilíndric, disposat de manera que l’aire de l’interior pugui vibrar i, així, pugui produir sons.
Les parets del tub són rígides, i a la base hi ha una embocadura per on és insuflat l’aire Això produeix la vibració d’aquest aire, les característiques de la qual depenen fonamentalment de les dimensions i de la forma del tub també varien segons que l’extrem superior sigui obert o tancat Quan l’aire del tub vibra, es produeixen —com en el cas de les cordes— ones estacionàries Si el tub és tancat per un extrem, les ones presenten en aquest punt un node, mentre que a l’extrem oposat apareix un ventre en aquest cas la longitud d’ona λ de la vibració val λ = 4 L, L essent la longitud del tub…
harmònic | harmònica
Música
Dit dels sons secundaris o concomitants en els quals es descompon un so musical.
Es produeixen en forma de sèrie ascendent que sona juntament amb el so fonamental sovint no són identificables, excepte per experts, o no són percebuts, a causa de llur feblesa Els harmònics inferiors són uns sèrie de sons que tenen entre ells les mateixes distàncies de la sèrie ascendent Harmònics instrumentals són obtinguts pe la vibració d’una determinada part d’un cos sonor i són els únics que es poden considerar com a parcials
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que correspon al…
distorsió
Física
Tecnologia
Deformació d’una imatge (per imperfeccions del sistema òptic utilitzat), del so, d’una vibració, d’un senyal elèctric, etc, a causa de les imperfeccions de l’aparell reproductor o amplificador, o bé en una transmissió.
Generalment la distorsió modifica la forma d’ona en electrònica i electroacústica s’esdevé molt sovint i segons els efectes produïts rep diversos noms distorsió d’amplitud, distorsió harmònica, distorsió de cruïlla , etc Hom parla de distorsió d’amplitud quan els diferents components de freqüència del senyal són amplificats o atenuats de forma desigual La distorsió harmònica es produeix quan en amplificar un senyal s’hi afegeixen harmònics d’ordre superior la qualitat d’un amplificador d’alta fidelitat depèn de la distorsió harmònica total , que és el tant per cent que representa…
fonamental
Música
Dit del so bàsic d’un acord.
També és aplicable al so generador de la sèrie dels harmònics i al so bàsic d’una escala modal, habitualment anomenat nota final o tònica
harmònic
Física
Matemàtiques
Cadascun dels termes de la sèrie de Fourier d’una funció periòdica (anàlisi de Fourier).
El terme de la sèrie de freqüència més baixa és anomenat harmònic fonamental o primer harmònic , i els altres termes són anomenats harmònics del fonamental
Heinrich Eduard Heine
Matemàtiques
Matemàtic alemany.
Investigà els harmònics esfèrics i la teoria de conjunts Establí el teorema que després fou estudiat per EBorel i HLebesgue, anomenat de Heine-Borel o de Borel-Lebesgue
Joseph Sauveur
Física
Matemàtiques
Físic i matemàtic francès.
És considerat un dels fundadors de l’acústica musical estudià l’orella humana i explicà la natura dels sobretons Investigà els tubs sonors, les cordes vibrants i els harmònics
timbre
Física
Música
Qualitat d’un so que permet distingir-lo dels altres que tenen idèntica altura i intensitat.
El timbre depèn de factors complexos acústicament nombre d’harmònics que formen el so, llur intensitat i selecció El timbre és modificat per la manera d’atacar o extingir el so