Resultats de la cerca
Es mostren 174 resultats
decibel
Música
Unitat relativa d’intensitat acústica.
Com a unitat relativa, el decibel dB no té dimensions, ja que és un nombre que prové del quocient entre dues quantitats corresponents a una mateixa magnitud pressió, potència o intensitat acústica En general, una de les quantitats és un valor de referència establert per alguna norma internacional Si s’anomena A la magnitud a mesurar, els decibels corresponents són deu vegades el logaritme decimal d’aquest quocient 10 logA/Aref Quan es parla de decibel de pressió o d’intensitat sonora, el valor de referència és el que correspon al llindar d’audibilitat d’un so pur de 1000 Hz La utilització d’…
mel
Música
Unitat subjectiva de mesura de l’acuïtat d’un so pur.
Es defineix de tal manera que una duplicació de mels es correspon amb la percepció d’un interval d’octava Així, el marge auditiu humà que va dels 16 Hz als 16000 Hz de mitjana és de 2400 mels El valor 1000 mels es fa correspondre amb la freqüència de 100 Hz La necessitat d’una unitat subjectiva per a l’acuïtat prové del fet que la detecció de les fluctuacions d’un to depèn de la seva freqüència En general, l’oïda humana és més sensible a les fluctuacions dels tons aguts que a les dels greus Així, es poden detectar canvis de l’ordre del 0,5% per a freqüències superiors a 1000 Hz, mentre que…
tactus
Música
En la música dels segles XV i XVI, terme equivalent a l’actual pulsació1, tant en el sentit d’unitat de temps com en el de gest propi del director o, més en general, del músic per a marcar aquesta unitat -el mateix terme tactus, literalment ’tacte', ja ho suggereix-.
A diferència, però, de la pulsació actual -unitat de temps relativa, estretament lligada al tempo i al caràcter de cada peça-, el tactus era una unitat de temps relativament fixa, d’entre 1/60 i 1/70 minuts Alguns estudiosos i teòrics han volgut veure en aquesta equivalència una certa relació entre tactus i ritme cardíac Fos com fos, aquesta relativa fixació del tactus implicà l’existència, durant el Renaixement, d’una mena de tempo ’usual', uniforme i constant en tota la música, amb possibles però molt lleugeres desviacions En la partitura, la nota que normalment representava el tactus era…
motiu
Música
La unitat formal amb sentit musical més elemental i, per tant, no descomponible en unitats més petites que mantinguin sentit musical.
Un motiu pot tenir diverses dimensions, però acostuma a estar compost per dues o més notes, a presentar una figura rítmica pròpia, que inclou una unitat de temps mètricament accentuada, i a ser fàcilment identificable ex 1 Tot i el seu valor nuclear, s’accepta que alguns motius es puguin descompondre en elements sense valor formal, coneguts com a cèllules ex 2 Exemple 1 - L van Beethoven Sonata op 2 , núm 2, Scherzo © Fototecacat/ Jesús Alises D’altra banda, el motiu és un element formal amb sentit però no autosuficient i, per tant, queda comprès en una unitat formal…
treset
Música
Grup irregular que resulta de dividir en tres una pulsació (una unitat mètrica qualsevol) que normalment, segons el que prescriu l’indicador mètric de la peça, s’hauria de dividir en dos.
La figura que representa cada una de les noves divisions és la mateixa que fins aleshores representava una unitat mètrica del mateix nivell S’indica amb la xifra 3, sovint acompanyada d’un claudàtor horitzontal, a sota o a sobre del grup
anacrusi
Música
Nota o grup de notes que precedeix el primer accent mètric (ictus inicial, temps fort, caiguda, etc.) d’una unitat formal qualsevol (frase, motiu, període, etc.).
Hom pot anomenar també crusi la nota que coincideix amb l’accent mètric inicial, i metacrusi la nota o grup de notes que la segueixen Atès, d’una banda, que una anacrusi ho és amb relació a un determinat accent mètric -que cal entendre com el més important de la unitat formal considerada- i, de l’altra, que els accents mètrics formen un sistema jeràrquic uns són més importants que uns altres, els quals, al seu torn, encara ho són més que uns altres, etc hom pot concloure que l’aparició d’anacrusis és possible a tots nivells Dit d’una altra manera les anacrusis són sempre…
doset
Música
Grup irregular que es forma en dividir en dos una pulsació (una unitat mètrica qualsevol) que normalment, segons el que prescriu l’indicador mètric de la peça, s’hauria de dividir en 3, 5, etc.
La figura que representa cada una de les noves divisions és, en general, la mateixa que fins aleshores representava una unitat mètrica del mateix nivell S’indica amb la xifra 2, sovint acompanyada d’un claudàtor horitzontal, a sota o a sobre del grup
quatret
Música
Grup irregular que es forma en dividir en quatre una pulsació (una unitat mètrica qualsevol) que normalment, segons el que prescriu l’indicador mètric de la peça, s’hauria de dividir en cinc, sis, etc.
La figura que representa cadascuna de les noves divisions és la mateixa que fins aleshores representava una unitat mètrica del mateix nivell quatre semicorxeres en lloc de sis en compàs de 6/8, per exemple Per a molts teòrics és simplement un cas particular de doset cadascun dels dos valors característics del doset dividits per dos S’indica amb la xifra 4, sovint acompanyada d’un claudàtor horitzontal, a sota o a sobre del grup
cinquet
Música
Grup irregular que es forma en dividir en cinc una pulsació (una unitat mètrica qualsevol) que normalment -sigui perquè ho prescriu l’indicador mètric de la peça, o bé per la divisió normal de les figures- s’hauria de dividir en 2, 3, etc.
La figura que representa cada una de les noves divisions és, normalment, la mateixa que fins aleshores representava una unitat mètrica del mateix nivell S’indica amb la xifra 5, sovint acompanyada d’un claudàtor horitzontal, a sota o a sobre del grup
grup irregular
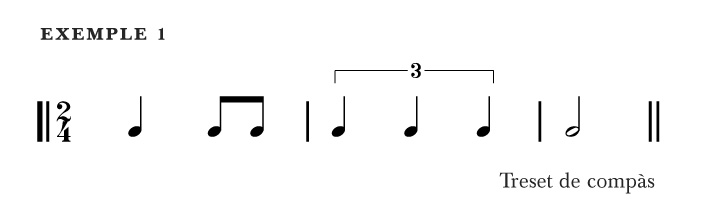
Exemple 1
© Fototeca.cat/ Jesús Alises
Música
Nom amb què alguns teòrics de la música designen aquells grups de figures que impliquen una divisió de la unitat mètrica que les inclou -compàs, temps, divisió del temps, etc.- diferent de la que prescriu l’indicador mètric de la peça.
Els exemples més comuns són el doset, el treset, el siset, etc A la partitura, s’indica amb una xifra -sovint acompanyada d’un claudàtor horitzontal a sota o a sobre del grup- que determina la nova divisió La figura que representa cada una d’aquestes noves divisions és, en general, la mateixa que fins aleshores representava una unitat mètrica del mateix nivell L’ús d’aquesta notació no es generalitzà fins al segle XIX, però amb anterioritat existien nombrosos exemples d’interpretació irregular de grups amb notació regular El cas més freqüent és l’acomodament de ritmes binaris a ritmes…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina