Resultats de la cerca
Es mostren 27 resultats
diferencial
Física
Dit dels instruments que serveixen per a mesurar la diferència entre dues magnituds, però no llurs valors absoluts.
Per exemple, el baròmetre diferencial mesura la diferència entre la pressió al nivell de la mar i l’existent al lloc on hom efectua la mesura
tub de Pitot
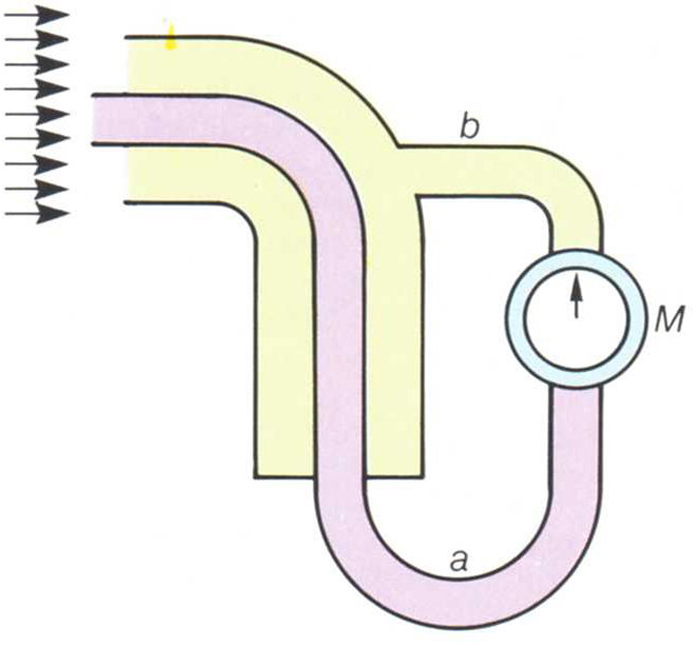
Esquema d’un tub de Pitot: el manòmetre diferencial M mesura la diferència entre la pressió dinàmica (que mesura pel tub a) i la pressió estàtica (que mesura pel tub b) del fluid, el moviment del qual és assenyalat per les fletxes
©
Física
Instrument que permet de mesurar la velocitat d’un fluid respecte a un cos immòbil o la d’un mòbil al si d’un fluid.
Consisteix en dos tubs coaxials doblegats en angle recte, de manera que un dels braços sigui parallel al corrent del fluid o a la direcció del mòbil El tub exterior, que és tancat per tots dos extrems i connectat a un manòmetre diferencial per un orifici lateral, enregistra la pressió estàtica, P e , és a dir, la pressió del medi ambient El tub interior, connectat al manòmetre per l’extrem oposat al d’entrada del fluid, enregistra la pressió dinàmica del corrent, P d , funció de la velocitat El manòmetre diferencial, en donar la diferència d’ambdues pressions, indica…
condicions de contorn
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui uns determinats valors en punts o zones concrets del domini de valors de la variable independent, zones anomenades contorns del problema.
Per exemple, el potencial electroestàtic d’una distribució de càrregues elèctriques ha de satisfer l’equació diferencial de Laplace ∇ 2 V =0 amb la condició de contorn que V sigui constant sobre la superfície dels conductors que hi hagi a l’espai del problema Les condicions de contorn són imposades per les lleis físiques, per la simetria o per la disposició experimental del problema Si el problema dinàmic és controlat per una o diverses equacions diferencials en derivades parcials, la solució particular del problema generalment ha de satisfer, a més d’unes condicions de contorn,…
braquistòcrona
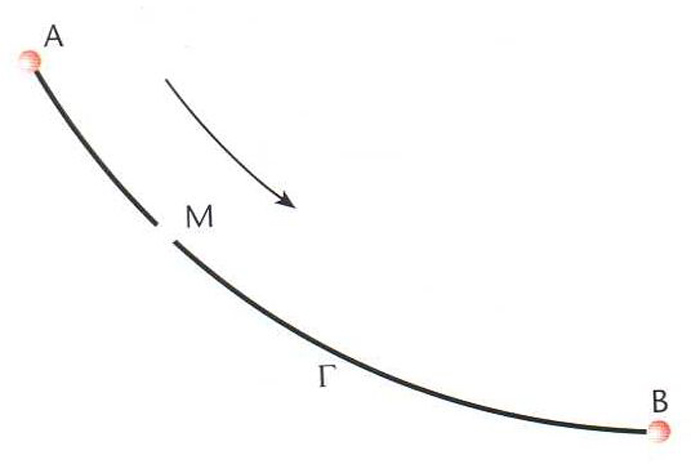
Braquistròcrona
© fototeca.cat
Física
Corba que ha de recórrer una partícula que parteix del repòs i es mou per l’acció del pes i sense fregament, per tal d’unir dos punts fixs A
i B
en el mínim de temps possible.
La solució de l’eqüació diferencial que explicita analíticament el problema és una cicloide El problema de trobar aquesta corba és famós en la història de la matemàtica, car conduí Johann Bernoulli a l’establiment formal del càlcul de variacions variació
cèl·lula de Barton
Física
Convertidor de diferències de pressió en petits desplaçaments angulars, format per dues cambres elàstiques plenes d’oli de silicona, separades per un sistema hidràulic.
El desplaçament de les dues cambres és transmès a un eix giratori per l’acció d’una politja La cèllula de Barton és molt emprada com a detector de la pressió diferencial en els cabalímetres basats en la diferència de pressió generada per un element d’estrangulació
equació de Navier-Stokes
Física
Expressió matemàtica de l’equilibri dinàmic d’un element de fluid, que en el cas particular d’un corrent de fluid newtonià (viscositat cinemàtica constant), en règim laminar, pren la forma
.
v essent la velocitat, F la força activa aplicada a la unitat de massa, ρ la densitat, p la pressió, γ la viscositat cinemàtica, i ∇ l’operador diferencial nabla D’aquesta fórmula hom pot deduir l’equació fonamental de la hidroestàtica, en fer γ = 0 fluid perfecte i ∂ν/∂ t = 0 fluid en repòs o en moviment continu
calor d’adsorció
Física
Calor despresa en el procés d’adsorció d’un mol de substància sobre la superfície d’un adsorvent.
Hom distingeix la calor integral i la calor diferencial d’adsorció, anàlogament a com ho fa en el procés de dissolució La magnitud de les calors integrals d’adsorció oscilla entre 2 i 6 kcal/mol en els processos d’adsorció física, però assoleix valors que arriben a 100 kcal/mol en els d’adsorció química, d’ordre de magnitud anàleg als de les calors que entren en joc en les reaccions químiques
Antoine-César Becquerel
Física
Físic francès.
Estudià a l’École Polytechnique Fou oficial de l’exèrcit napoleònic, però deixà el càrrec per tal de dedicar-se a la ciència Descobrí la piezoelectricitat 1819 i inventà un galvanòmetre diferencial, una balança electromagnètica i un termoaparell És considerat un dels fundadors de l’electroquímica, a causa dels seus estudis relatius al recobriment de metalls amb níquel i cobalt per protegir-los, i amb manganès, ferro o òxid de plom, per acolorir-los Fou professor del Musée d’Histoire Naturelle
Josep Maria Plans i Freyre
Astronomia
Física
Físic i astrònom.
Estudià a la Universitat de Barcelona fou professor de física i química a l’institut de Castelló de la Plana, catedràtic de mecànica a la Universitat de Saragossa i de mecànica celeste a la de Madrid Publicà el 1913 Lecciones de termodinámica , fruit de la seva docència a Saragossa, i el 1921 Nociones fundamentales de mecánica relativista y proceso histórico del cálculo diferencial absoluto y su importancia actual El 1918 obtingué un premi de l’Institut d’Estudis Catalans per l’estudi Ellipsoide de Dirichlet
equació de Helmholtz
Física
Equació diferencial en derivades parcials que té per expressió
on k és un escalar.
Apareix a l’hora de cercar solucions de les equacions d’ones