Resultats de la cerca
Es mostren 143 resultats
llei de Moseley
Física
Llei segons la qual la freqüència ν de les ratlles dels espectres d’emissió o absorció de raigs X dels elements químics és ν = KZ2, essent K una constant i Z el nombre atòmic.
Aquesta llei experimental, que demostrà que el nombre atòmic d’un àtom era igual al d’electrons que envolten el nucli, pot ésser deduïda formalment de la teoria de l' àtom de Bohr , d’on resulta que essent R la constant de Rydberg , c la velocitat de la llum, i x i y els valors dels nombres quàntics principals de les òrbites entre les quals “salta” un electró en ésser excitat espectre d’absorció o desexcitat espectre d’emissió
nònius
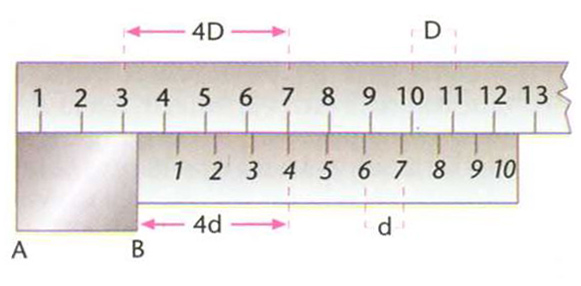
Mesra de la longitud AB d’un objecte amb nònius: als 3mm que dona el regle principal, hi cal afegir =,4 mm (essent D = 1mm i d =0,9mm, 4D - 4d =4(d-d)= 0,4mm
© Fototeca.cat
Física
Instrument per a mesurar longituds amb precisió.
És anomenat també vernier Consta essencialment d’un regle principal , graduat normalment en millímetres, sobre el qual llisca un segon regle, el nònius pròpiament dit, que té una longitud de 9 mm i és dividit en 10 parts Per a mesurar la longitud d’un objecte, hom el colloca sobre el regle principal i fa córrer el nònius fins a tocar l’objecte El número d’ordre de la divisió del nònius que coincideix amb una divisió del regle principal és el nombre de dècimes de millímetre que l’objecte sobrepassa la divisió del regle principal, que, per defecte, indica la longitud en millímetres de l’…
factor giromagnètic
Física
Quocient entre el moment magnètic i el moment angular d’un cos elèctricament carregat: g=μ/L.
En mecànica clàssica, g = q / 2m, essent m la massa del cos en qüestió i q la seva càrrega elèctrica En mecànica quàntica l’expressió continua essent vàlida per als moments magnètics associats als moments angulars orbitals, però no pas per als moments magnètics associats al spin, que depenen del tipus de partícula
absorbància
Física
Magnitud que caracteritza una substància pel que fa a l’absorció d’energia radiant.
Ve donada per A = log I 0 / I , essent I 0 i I les intensitats radiants incident i transmesa, respectivament Si la llum és monocromàtica es verifica, generalment, que A d , essent d el gruix travessat llei de Lambert i, en el cas de solucions, A cd , on c és llur concentració llei de Beer
teorema de Bloch
Física
Teorema segons el qual les solucions de l’equació de Schrödinger per a un electró que es mou en el si d’un potencial periòdic (p ex, el potencial en un cristall) és periòdic respecte a translacions T sobre la malla: U (r + T = U (r)) satisfan l’expressió.
ψ r + T = e i k T ψ r , essent k el vector d’ona aquestes funcions s’anomenen funcions de Bloch Una expressió equivalent a l’anterior és ψ k, r = e i k r u k, r , essent u una funció amb la mateixa periodicitat que el potencial u k, r + T = u k, r La funció d’ona ψ és, doncs, una ona plana modulada a cada cella per la funció periòdica u k, r Aquest teorema rep a vegades el nom de teorema de Floquet
llei de Biot i Savart
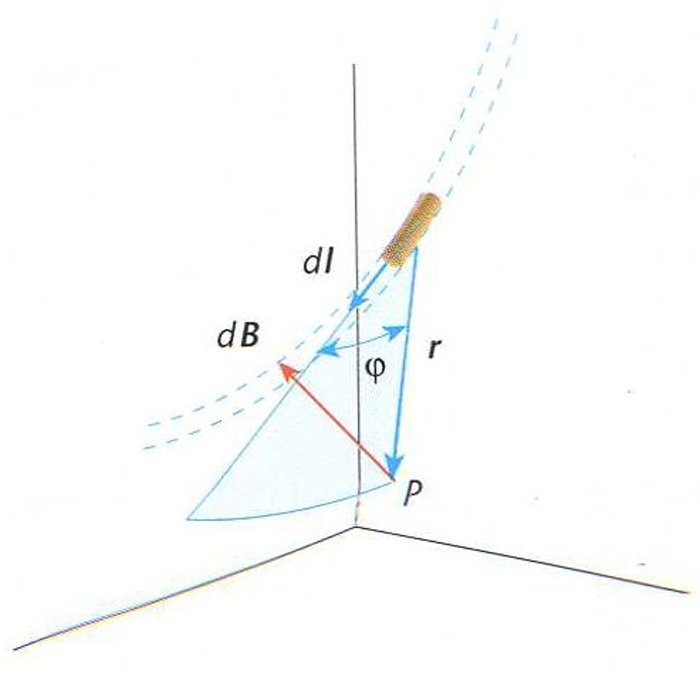
Llei de Biot i Savart
© Fototeca.cat
Electrònica i informàtica
Física
Llei que dóna la inducció magnètica dB en un punt qualsevol P de l’espai, produïda per un element de corrent Idl que circula per un conductor:
essent μ 0 la permeabilitat magnètica del buit, I la intensitat del corrent, r la distància de l’element de corrent a P i θ l’angle entre els vectors d l i r En forma vectorial s’expressa per El camp total, suma de les contribucions de tots els elements de corrent es calcula fent Si el conductor és rectilini, aquesta expressió dóna el resultat essent R la distància perpendicular entre el conductor i el punt P en qüestió Quan les condicions de simetria ho permeten el camp magnètic pot calcular-se mitjançant el teorema d’Ampère
principi de Bernoulli
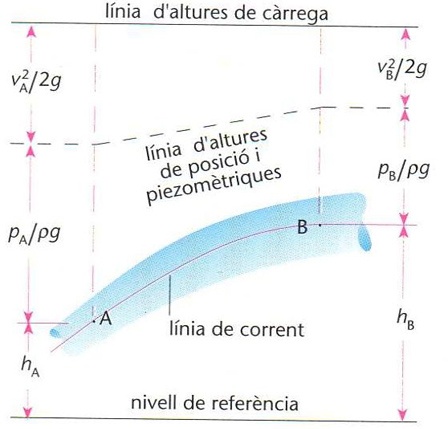
Representació del principi de Bernoulli com a constància de l’altura de càrrega, a partir de l’altura de posició h, l’altura piezomètrica P/pg (P, pressió mesurada amb un manòmetre; p, densitat del fluid; g, acceleració de la gravetat) i l'altura dinàmica v2/2g (v, velocitat del fluid)
Física
Expressió matemàtica de la llei de conservació de l’energia per a fluids perfectes (és a dir, no viscosos) i incompressibles que circulen en règim estacionari, formulada per Daniel Bernoulli a Hydrodinamica (1738).
En produir-se en un fluid un corrent estacionari, la suma de la pressió estàtica P+ρgy essent P la pressió, ρ la densitat del fluid, g l’acceleració de la gravetat i y l’altura sobre algun nivell de referència i de la pressió dinàmica ρn 2 /2 essent v la velocitat es manté constant al llarg d’una línia de corrent L’expressió matemàtica del teorema és P+ρgy+ρv 2 /2 = constant Hom defineix l' altura piezomètrica P/ρg i l’ altura dinàmica v 2 /2 g L’equació pot ésser generalitzada per a fluids no estacionaris, compressibles o viscosos
constant de desintegració
Física
Coeficient de proporcionalitat que relaciona el nombre de nuclis que es desintegren per unitat de temps amb el nombre de nuclis presents en aquell instant.
L’expressió matemàtica és donada per l’equació dn = λ n , λ essent la constant de desintegració, n , el nombre de nuclis presents, i dn , el nombre de nuclis que desapareixen el signe negatiu indica el fet de la minva del nombre de nuclis La variació de l’activitat en el temps, funció del nombre de nuclis, va relacionada amb la integral de l’anterior equació, l’expressió de la qual és nt = n₀e -λt , n₀ essent el nombre de nuclis en l’instant inicial, i t , el temps transcorregut des d’aquest instant inicial Unes magnituds derivades de la constant de desintegració…
equació de Laplace
Física
Matemàtiques
Equació diferencial en derivades parcials expressada per la fórmula Δf = 0, Δ essent el laplacià.
Les funcions que són solució de l’equació de Laplace són anomenades funcions harmòniques , i tenen una especial aplicació en la teoria del potencial En el cas que f sigui una funció de la variable complexa z = x + iy , l’equació de Laplace, que en aquest cas pren la forma ∂ 2 f /∂ x 2 + ∂ 2 f /∂ y 2 = 0, expressa la condició necessària i suficient perquè f sigui derivable
àtom de Bohr
Física
Model atòmic proposat per N.H.D. Bohr el 1913 per a descriure l’àtom d’hidrogen.
Recolza sobre les hipòtesis següents l’àtom només pot existir en uns certs estats estacionaris, caracteritzats pel fet que el seu electró només pot ocupar unes òrbites o nivells energètics ben definides, que, tot i ésser governades per la mecànica clàssica, són determinades per la condició que el moment angular orbital de l’electró sigui un múltiple enter de la constant de Planck reduïda L = nh , essent h = h/ 2π l’emissió i absorció d’energia per l’àtom no es realitza de forma contínua , com demanaria l’electrodinàmica clàssica en explicar el moviment circular dissipatiu d’un…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina