Resultats de la cerca
Es mostren 92 resultats
fórmula de Rayleigh
Física
Expressió formal que dóna la densitat d’energia d’una radiació per unitat d’energia i d’interval de freqüències a partir de la teoria del cos negre.
Fou emesa per J Rayleigh i J Jeans, al començament del segle, en l’àmbit de la mecànica clàssica, en la qual suposaven que els fotons eren com oscilladors clàssics amb una energia mitjana de kT principi d’equipartició de l’energia Hom l’escriu com ρ Τ ν = 8πν 2 / c 3 kT , on ν és la freqüència, c la velocitat de la llum, k la constant de Boltzmann i T la temperatura absoluta, i és l’expressió asimptòtica de la fórmula de Planck en la regió de les freqüències baixes h ν > ckT
principi de Bernoulli
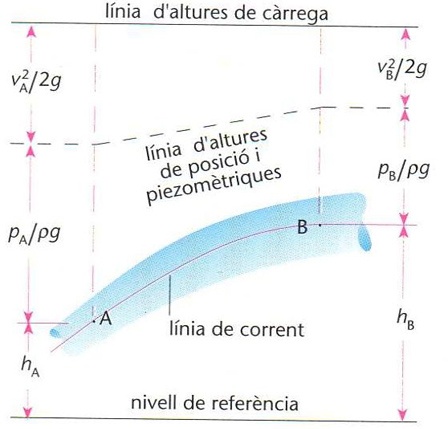
Representació del principi de Bernoulli com a constància de l’altura de càrrega, a partir de l’altura de posició h, l’altura piezomètrica P/pg (P, pressió mesurada amb un manòmetre; p, densitat del fluid; g, acceleració de la gravetat) i l'altura dinàmica v2/2g (v, velocitat del fluid)
Física
Expressió matemàtica de la llei de conservació de l’energia per a fluids perfectes (és a dir, no viscosos) i incompressibles que circulen en règim estacionari, formulada per Daniel Bernoulli a Hydrodinamica (1738).
En produir-se en un fluid un corrent estacionari, la suma de la pressió estàtica P+ρgy essent P la pressió, ρ la densitat del fluid, g l’acceleració de la gravetat i y l’altura sobre algun nivell de referència i de la pressió dinàmica ρn 2 /2 essent v la velocitat es manté constant al llarg d’una línia de corrent L’expressió matemàtica del teorema és P+ρgy+ρv 2 /2 = constant Hom defineix l' altura piezomètrica P/ρg i l’ altura dinàmica v 2 /2 g L’equació pot ésser generalitzada per a fluids no estacionaris, compressibles o viscosos
teorema de Bloch
Física
Teorema segons el qual les solucions de l’equació de Schrödinger per a un electró que es mou en el si d’un potencial periòdic (p ex, el potencial en un cristall) és periòdic respecte a translacions T sobre la malla: U (r + T = U (r)) satisfan l’expressió.
ψ r + T = e i k T ψ r , essent k el vector d’ona aquestes funcions s’anomenen funcions de Bloch Una expressió equivalent a l’anterior és ψ k, r = e i k r u k, r , essent u una funció amb la mateixa periodicitat que el potencial u k, r + T = u k, r La funció d’ona ψ és, doncs, una ona plana modulada a cada cella per la funció periòdica u k, r Aquest teorema rep a vegades el nom de teorema de Floquet
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que correspon al…
fórmula de Clairaut
Física
Fórmula que dóna el valor de l’acceleració de la gravetat g en un punt de latitud φ.
L’expressió teòrica és g = g e 1 + 5ω 2 a /2 g e - e sin 2 φ, on g e és el valor de la gravetat a l’equador, a és el semieix major equatorial de l’ellipsoide de referència, e és la seva ellipticitat i w és la velocitat angular de la Terra El valor numèric és donat per l’expressió g = 978,049 1-0,0052884 sin 2 φ, on hom ha pres com a ellipsoide de referència un d’aplatament 1/297
constant de desintegració
Física
Coeficient de proporcionalitat que relaciona el nombre de nuclis que es desintegren per unitat de temps amb el nombre de nuclis presents en aquell instant.
L’expressió matemàtica és donada per l’equació dn = λ n , λ essent la constant de desintegració, n , el nombre de nuclis presents, i dn , el nombre de nuclis que desapareixen el signe negatiu indica el fet de la minva del nombre de nuclis La variació de l’activitat en el temps, funció del nombre de nuclis, va relacionada amb la integral de l’anterior equació, l’expressió de la qual és nt = n₀e -λt , n₀ essent el nombre de nuclis en l’instant inicial, i t , el temps transcorregut des d’aquest instant inicial Unes magnituds derivades de la constant de desintegració són la vida mitjana i el…
pressió osmòtica
Física
Química
Diferència de pressions que hi ha entre un costat i l’altre d’una membrana semipermeable (osmosi) que separa dues dissolucions de concentracions diferents quan el sistema és en equilibri.
L’expressió formal de la pressió osmòtica és l’anomenada fórmula de Van't Hoff
API
Física
Escala areomètrica deguda a l’American Petroleum Institute i elegida als EUA com a estàndard per als productes del petroli.
És donada per l’expressió Graus areomètrics API a 15°C = 141,5/pes específic — 131,5
laplacià
Física
Matemàtiques
Operador diferencial, representat pels símbols Δ, ∇ 2
o ∇·∇, que, en ésser aplicat sobre una funció real de diverses variables reals, f
(
x 1
,...,x n
), dóna lloc a la funció
.
És relacionat amb els operadors diferencials gradient i divergència per l’expressió Δ f = divgraf f
principi de D’Alembert
Física
Principi diferencial de la mecànica que permet, mitjançant l’addició de les forces d’inèrcia i les forces aplicades a un sistema, derivar les equacions del moviment d’un sistema no sotmès a forces de fricció i tal que el treball virtual de les forces de lligam s’anul·li.
De l’expressió inicial s’obtenen, en canviar a coordenades generalitzades d’un sistema conservatiu amb lligams holònoms, les equacions de Lagrange
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina