Resultats de la cerca
Es mostren 5 resultats
palanca
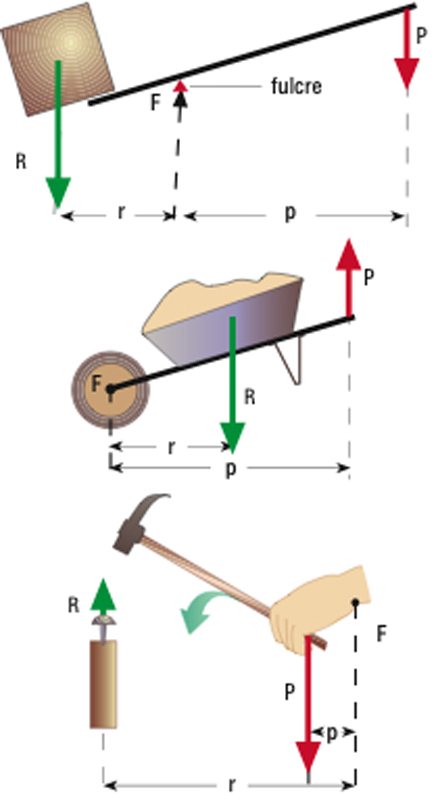
A dalt, palanca de primer gènere (alçaprem); al centre, de segon gènere (carretó); a baix, de tercer gènere (martell)
© Fototeca.cat
Física
Màquina simple que pot ésser esquematitzada en una barra rígida, mòbil al voltant d’un punt de suport o fulcre, que permet de vèncer un esforç, anomenat resistència, en aplicar-n’hi un altre, anomenat potència.
Segons la posició relativa dels punts on hom aplica la potència i la resistència i el punt de suport, les palanques són classificades en tres gèneres diferents en la palanca del primer gènere, el punt de suport és situat entre els d’aplicació de la potència i de la resistència en la del segon, la resistència és aplicada entre el punt de suport i el d’aplicació de la potència i en la del tercer, la potència és aplicada entre la resistència i el punt de suport Del primer gènere deriven l’alçaprem, la balança de braços iguals o la romana, del segon el trencanous, i del tercer els molls La llei…
mecànica quàntica-relativista
Física
Part de la mecànica quàntica que inclou les teories de la relativitat.
La mecànica quàntica nasqué de la mecànica relativista L&de Broglie Però la dinàmica quàntica elaborada per Schrödinger utilitza l’expressió no relativista de l’energia cinètica dels corpuscles, cosa que s’acorda amb les velocitats modestes dels nuclis i els electrons atòmics als quals és aplicada PAMDirac fundà la mecànica quàntica relativista 1929 en crear una funció d’ona de quatre components, un per cada dimensió espacial x, y i z i un per la dimensió temporal, el temps t No es tracta, però, d’un vector, ans d’un ésser matemàtic nou, dit spinor Dirac trobà el sistema de quatre…
estadística de Bose-Einstein
Física
Estadística quàntica que regeix el comportament d’un conjunt de bosons indiscernibles i independents (mecànica estadística).
Els bosons no obeeixen el principi d’exclusió de principi d’exclusió de Pauli i, per tant, n'hi pot haver un nombre qualsevol en un mateix estat quàntic Hom pot demostrar que el nombre mitjà de bosons en l’estat d’energia E és essent k la constant de Boltzmann, T la temperatura absoluta del sistema i μ una constant determinada per la condició Σ n E = N , on N és el nombre total de partícules del conjunt
estadística de Fermi-Dirac
Física
Estadística que regeix la distribució d’un conjunt de fermions en funció dels possibles valors de l’energia i de les posicions.
Té en compte les regles quàntiques, i el principi d’exclusió de Pauli Quan un conjunt de partícules és regit per l’estadística de Fermi-Dirac, la seva funció d’ona total és antisimètrica respecte a l’intercanvi de dues de les partícules és a dir, que canvia de signe sota l’intercanvi de les dues partícules La funció de distribució és la distribució de Fermi-Dirac
estadística de Maxwell-Boltzmann
Física
Estadística que regeix la distribució d’un conjunt de partícules en funció dels possibles valors de l’energia tenint en compte els principis de la mecànica clàssica.
Utilitzada inicialment per a descriure el comportament dels gasos ideals, hom l’aplicà, per extensió, a l’estudi del gas electrònic dels metalls, on començà a fallar, pel fet que aquesta estadística ignora les lleis quàntiques per analitzar aquests casos han estat desenvolupades altres estadístiques, com la de Bose-Einstein i la de Fermi-Dirac L’estadística de Maxwell-Boltzmann ha permès, però, de construir un model, el de gas ideal, on es reflecteix completament el sistema formal de la termodinàmica clàssica i d’on hom pot extreure una interpretació probabilística de l' entropia