Resultats de la cerca
Es mostren 3269 resultats
primer element
Matemàtiques
En un conjunt ordenat OOOX,≤OOO, un element x ∈ X és el primer element d’X si, i només si, per a tot altre element y ∈ X,x ≤ y
.
element recíproc
Matemàtiques
Nom que hom acostuma a donar a l’invers quan indica l’operació ⋅ i l’element neutre per 1.
En aquest cas, l’invers d' x és indicat per x -1
element invers
Matemàtiques
En una estructura algèbrica OOOE,*,eOOO l’invers d’un element x∈ E és un element OOO x∈ E tal que x * OOO = e = OOO * x, on e és un element neutre.
element oposat
Matemàtiques
Nom que hom acostuma a donar a l’element invers en una estructura algèbrica associativa: x*(y*z) = (x*y)*z, commutativa: x*y = y*x i amb un element neutre, i hom sol designar-la per 0.
Normalment, l’operació * és designada aleshores per + i l’invers OOO d' x , per − x
element infinitesimal
Matemàtiques
Element que, en valor absolut, és més petit que qualsevol nombre real estàndard i, en canvi, és no nul..
És la base conceptual de l’anàlisi no estàndard, intuïda per Wilhelm Gottfried Leibniz al segle XVII i, formalitzada per Abraham Robinson al començament dels anys seixanta, usa tècniques de teoria de models
element adherent
Matemàtiques
En un espai topològic OOOX,OOOooo, un element x ∈ X és adherent a un conjunt A ⊆ X si, i només si, tot entorn obert d’x talla a A
.
El conjunt de tots els punts adherents a A rep el nom d’adherència o clausura d' A i és designat Ā i es designat Ā i, a voltes, CL A És el més petit conjunt tancat que conté el conjunt A Un conjunt A és tancat per a la topologia OOO si, i només si, Ā =
darrer element
Matemàtiques
En un conjunt ordenat OOOX, ≤OOO, un element x ∈ X és el darrer element d’X si, i només si, per a tot altre element y ∈ X, x ≤ y
.
distribució
t
n
Matemàtiques
Siguin Y
i Z
variables aleatòries independents tals que Y
sigui N
(0,1) i Z
tingui una distribució x 2
amb n
graus de llibertat i hom consideri la variable aleatòria
Aquesta variable té la funció de distribució i densitat La funció de distribució S n x rep el nom de distribució t amb n graus de llibertat o de distribució Student amb n graus de llibertat en memòria de l’estadístic anglès WS Gosset, que escrigué amb el pseudònim de Student
llei normal
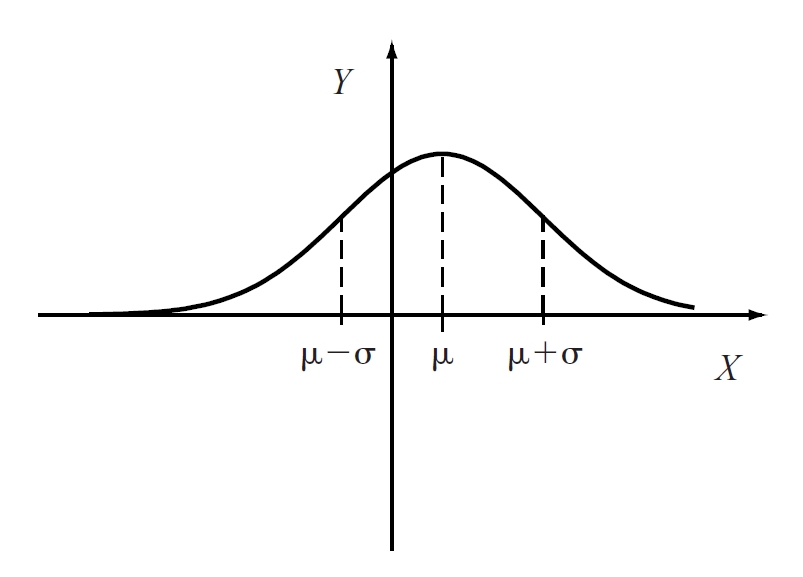
Llei normal de probabilitat de mitjana μ i desviació tipus σ
Fototeca.cat
Matemàtiques
Llei de probabilitat contínua i simètrica en la qual la mitjana, la moda i la mediana coincideixen i la funció de densitat té forma de campana de Gauss o corba normal.
Aquesta densitat depèn de dos paràmetres, la mitjana μ i la desviació típica σ En general, es caracteritza per N μ, σ i la seva funció de densitat val
distribució X
2
Matemàtiques
Si X 1
,..., X n
són n
variables aleatòries independents, totes de distribució N
(0,1), la variable
és una variable aleatòria i la seva distribució rep el nom de distribució x 2
amb n
graus de llibertat.
La funció de distribució rep el nom de distribució x 2 , essent k n x la funció de densitat