Resultats de la cerca
Es mostren 3270 resultats
mediana
Matemàtiques
En un conjunt de dades o d’observacions estadístiques, ordenades de menor a major, dada situada en el centre, és a dir, que té el mateix nombre de dades tant per sobre com per sota.
En el cas que el nombre de dades sigui parell, hom pren com a mediana la mitjana de les dues dades centrals
maximal
Matemàtiques
Dit de l’element a d’un conjunt ordenat C tal que no existeix en C cap altre element que sigui major que a
.
Tot element màxim és maximal, però no recíprocament
matroide
Matemàtiques
Estructura algèbrica consistent en un conjunt E i un conjunt S de parts no buides de E que satisfan: tot singletó de E pertany a S
.
Si X ∈S , aleshores tota part Y no buida de E inclosa en X pertany també a S i, per a tota part A de E , si X i Y són dos elements de S continguts en A i maximals, aleshores card X = card Y La teoria de matroides fou introduïda per Withney el 1935 i ha experimentat un desenvolupament ràpid en ésser aplicada als espais vectorials i a la teoria de grafs
corba d'ompliment
Matemàtiques
Corba contínua que passa per tots els punts d’una regió fins a omplirla enterament.
Les corbes d'ompliment més conegudes són les corbes de Peano
esfericon
Matemàtiques
Sòlid tridimensional d’una sola cara, dues arestes i quatre vèrtexs que s’obté de tallar un bicon circular recte de radi igual a l’altura amb un pla que en conté l’eix de rotació i d’ajuntar posteriorment les dues peces girant-ne una 90 graus.
sensedades
Matemàtiques
Valor convencional que s’assigna a una variable de la qual no es tenen dades, a fi d’evitar que prengui un valor per defecte o que quedi sense valor.
funció el·líptica de Weierstrass
Matemàtiques
Donat un subgrup discret de ℂ, Ω, generat per dos complexos independents, funció definida per
.
problema de Waring
Matemàtiques
Problema de la teoria de nombres proposat pel matemàtic anglès Edward Waring (Old Heath 1734-98) l’any 1770, consistent a demostrar que per a qualsevol nombre natural n existeix un nombre associat K (n), de manera que qualsevol natural pot ésser representat com una suma, com a màxim, de K (n) termes, cada terme essent una potencia n-èsima d’un natural.
En particular, cada nombre natural hauria de poder ésser representat com a suma de quatre quadrats com a màxim i com a suma de nou cubs Aquest problema fou resolt per Hilbert el 1909
diagrama de Venn
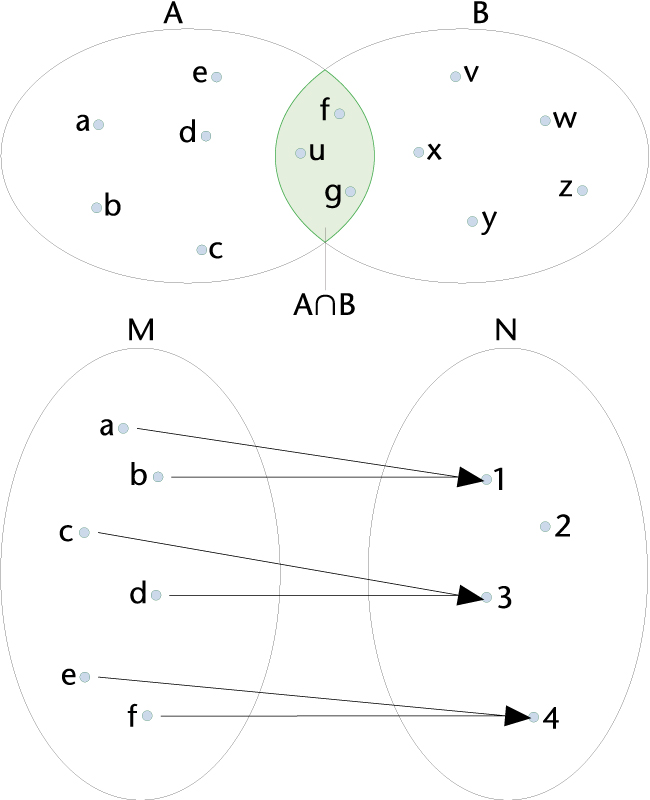
Representació de la intersecció dels conjunts A i B (a dalt) i de l’aplicació del conjunt M en el conjunt N (a baix) per mitjà de diagrames de Venn
© Fototeca.cat
Matemàtiques
Diagrama emprat amb fins didàctics per a representar gràficament conjunts i estudiar les relacions i operacions entre conjunts.
Aquests diagrames foren introduïts pel matemàtic i lògic anglès John Venn 1834-1923 Els conjunts són representats mitjançant cercles o corbes tancades qualssevol Cal no confondre un diagrama de Venn amb la regió del pla limitada pel diagrama És conegut també com a diagrama d’Euler-Venn