Resultats de la cerca
Es mostren 3270 resultats
superfície tangent a una altra superfície
Matemàtiques
Superfície que, en un punt o en diversos punts, té el mateix pla tangent de la superfície donada.
superfície reglada
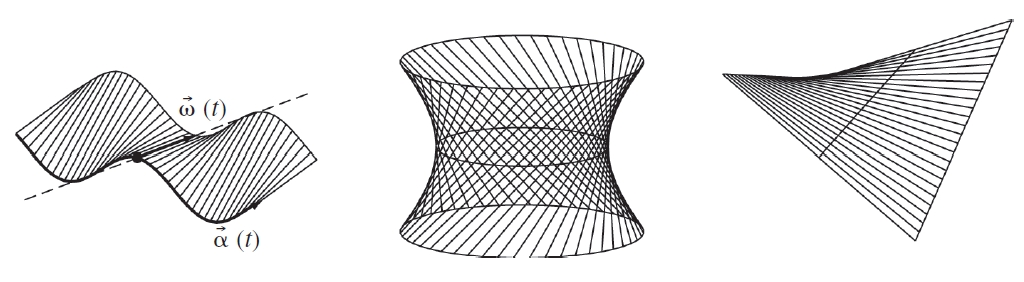
Superfícies reglades
Matemàtiques
Superfície engendrada per una família infinita de rectes que depenen d’un paràmetre.
Cadascuna d’aquestes rectes és anomenada generatriu de la superfície els procediments habituals per a definir-les són donar les equacions d’una recta en l’espai amb un paràmetre variable, o bé donar tres corbes directrius i prendre com a generatrius les rectes que recolzen sobre aquestes tres corbes Hi ha dues classes de superfícies reglades si en tots els punts d’una mateixa generatriu la superfície té el mateix pla tangent, es tracta d’una superfície desenvolupable , i la superfície pot ésser construïda cargolant oportunament un o diversos trossos de paper però si en cada punt d’una…
superfície helicoidal
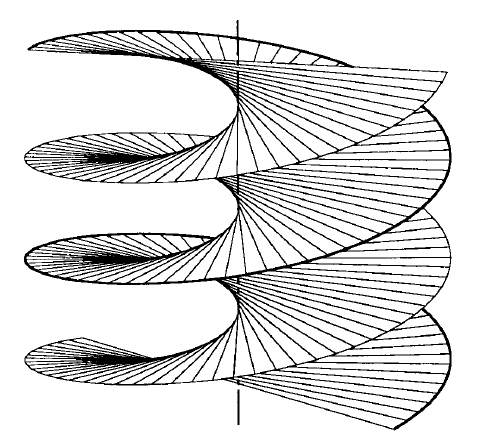
Superfície helicoïdal
Matemàtiques
Superfície reglada engendrada per una recta que es mou recolzant sobre l’hèlix i a l’eix de l’hèlix i sempre perpendicular a aquest eix.
Hom pot definir la superfície helicoidal ordinària com una superfície reglada que té per directrius una hèlix, el seu eix i la recta de l’infinit dels plans perpendiculars a l’eix És la superfície que conté les arestes dels graons d’una escala de cargol
superfície esfèrica
Matemàtiques
Superfície constituïda per tots els punts de l’espai que són a una distància (radi) fixa d’un punt fix (centre).
L’estudi de les figures que es poden traçar damunt una superfície esfèrica dóna lloc a la geometria esfèrica En són els elements fonamentals els punts i les circumferències màximes situades en plans que passen pel centre Figures importants són els triangles esfèrics , amb els quals hom pot fer càlculs per mitjà de la trigonometria esfèrica, que guarden un cert parallelisme amb els de la trigonometria plana La geometria esfèrica ha tingut un gran desenvolupament pel fet que la cosmografia estudia la posició dels astres com si fossin punts situats sobre una esfera de radi infinit i amb centre a…
superfície de revolució
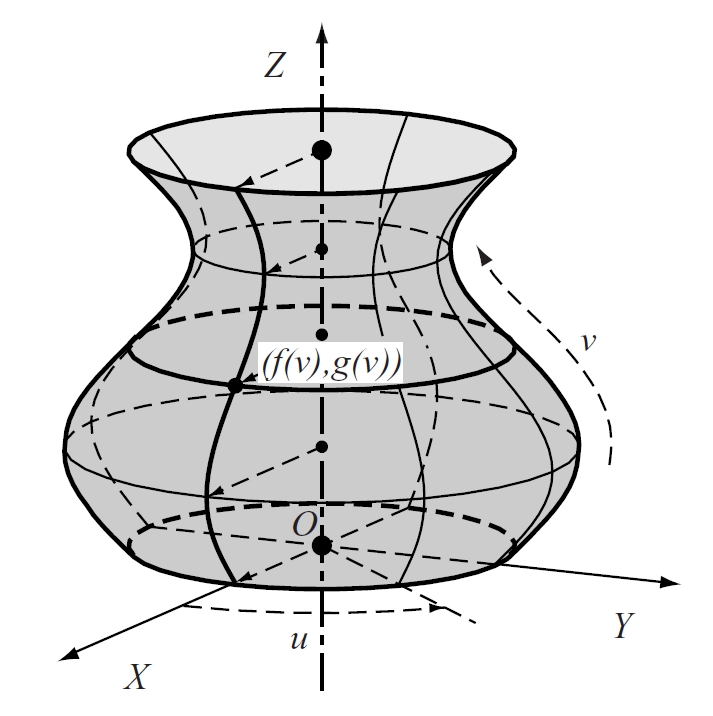
Superfície de revolució
Matemàtiques
Superfície engendrada per la rotació d’una corba (generatriu) entorn d’un eix, anomenat de revolució.
Si aquesta corba és plana i situada en un pla que conté l’eix és anomenada meridiana de la superfície La circumferència descrita per cada punt de la meridiana és anomenada parallel Els meridians i els parallels d’una superfície esfèrica són circumferències Els meridians de la superfície terrestre són aproximadament ellipses
superfície cilíndrica
Matemàtiques
Superfície engendrada per una família de rectes paral·leles entre elles que recolzen sobre una corba donada, plana o no, anomenada directriu de la superfície
.
El cas més simple superfície circular cilíndrica es presenta quan la corba directriu és una circumferència i les rectes generatrius són perpendiculars al pla de la circumferència
element de superfície
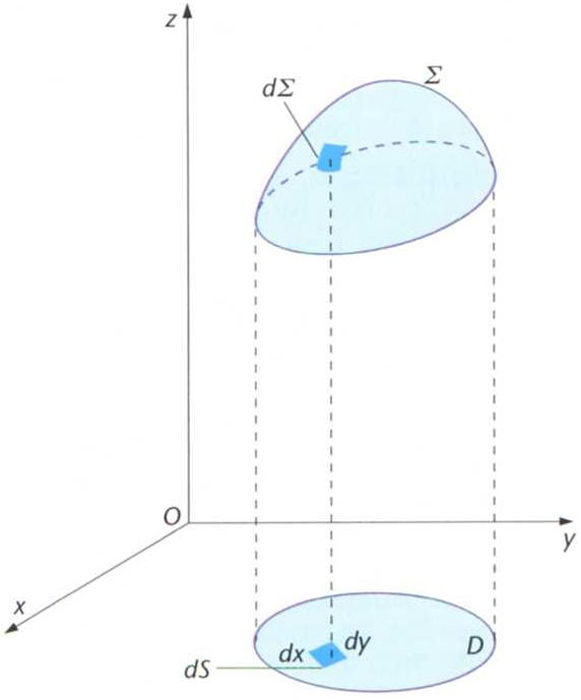
Element de superfície
© fototeca.cat
Matemàtiques
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
superfície
Matemàtiques
Conjunt de punts de l’espai que poden ésser determinats per dos paràmetres.
La manera més simple de determinar una superfície és donar una o més equacions del tipus z = f x,y Elegit un punt x,y en el domini de definició de la funció f , aquesta funció o aquestes funcions donen els valors de z , que, juntament amb x,y , són les coordenades cartesianes dels punts de la superfície Les funcions que donen la superfície esfèrica són , on el signe + correspon a l’hemisferi superior, i el signe - a l’hemisferi inferior L’equació z = ax + by + c correspon al pla o superfície plana Sovint és difícil, o impossible, d’expressar una superfície per mitjà de les seves equacions…