Resultats de la cerca
Es mostren 3270 resultats
espai de Baire
Matemàtiques
Espai topològic on la intersecció de tota família numerable d’oberts densos és densa en l’espai donat.
punts de Brocard
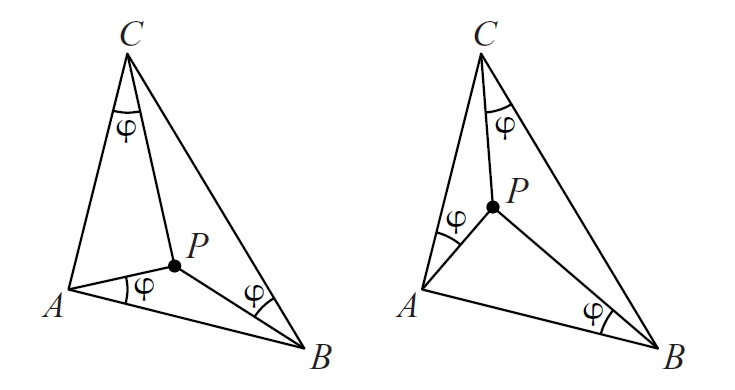
punts de Brocard
© fototeca.cat
Matemàtiques
Punts P d’un triangle ABC tals que els angles PBC, PCA i PAB són iguals.
En tot triangle n’hi ha dos
bosc
bosc
funcions de Bessel de primera classe
Matemàtiques
Solucions de l’equació diferencial de Bessel, de la forma
on Γ és la funció gamma.
J - n x n’és també una solució particular Si n és un nombre enter J - n x = -1 n J n x en canvi, si n no és enter J n x i J - n x són independents, de manera que la solució general de l’equació diferencial de Bessel és y x = aJ n x + bJ - n x ,en què a i b són constants
bicorne
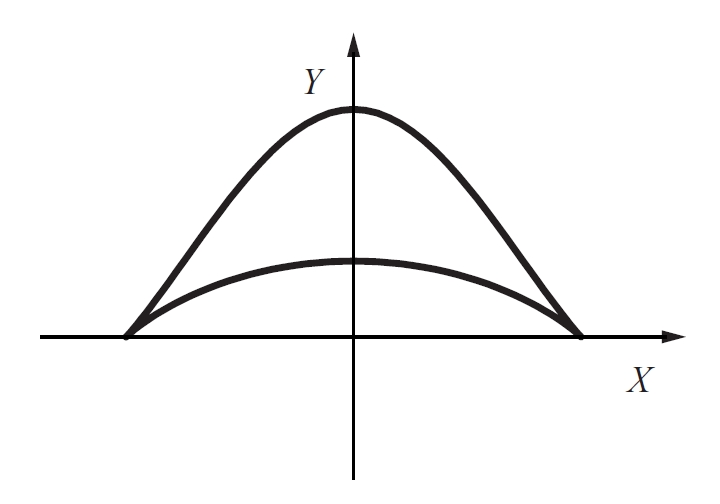
bicorne
Matemàtiques
Corba plana quàrtica definida per l’equació (x2 + 2ay - a2)2 = y2(a2-x2).
lemniscata de Bernoulli
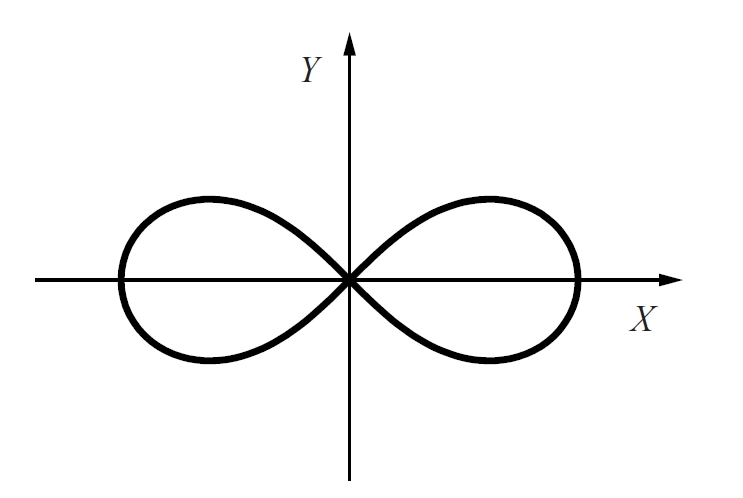
lemniscata de Bernoulli
Matemàtiques
Espiral sinusoïdal d’equació cartesiana (x2 + y2)2 = a2(x2 - y2).
És la inversa d’una hipèrbola equilàtera respecte del seu origen
nombre de Bell
Matemàtiques
Nombre de particions que es poden fer d’un conjunt de n elements. Aquest nombre es representa per Bn i valrepresenta el nombre d'Stirling.
El nombre de Bell queda determinat pel conveni B 0 i per la recurrència
axiomes independents
Matemàtiques
Conjunt d’axiomes tals que cap d’ells no es pot deduir dels altres.
Per a demostrar aquesta independència es donen models que satisfan certs axiomes, però no els altres
axiomes de separació
Matemàtiques
Axiomes topològics relatius a les possibles separacions entre punts.
En un espai topològic Y , els axiomes són Axioma T 0 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x que no conté y Axioma T 1 Per a qualsevol parell de punts x i y diferents, existeixen un entorn U de x , i un entorn V de y , tals que U no conté y i V no conté el punt x Quan aquest axioma se satisfà, l’espai es diu espai de Fréchet Axioma T 2 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x i un entorn de y sense punts en comú Quan aquest axioma se satisfà, l’espai s’anomena espai de Hausdorff Axioma T 3 Per a cada punt x i tot conjunt…
axiomes de numerabilitat
Matemàtiques
Axiomes topològics relatius a la numerabilitat de les bases d’entorns.
El primer axioma de numerabilitat en un espai topològic estipula que cada punt de l’espai té una base d’entorn numerable El segon axioma de numerabilitat postula l’existència d’una base d’oberts numerable en la topologia d’un espai topològic Si un espai topològic satisfà aquest segon axioma s’anomena separable