Resultats de la cerca
Es mostren 3270 resultats
màxim
Matemàtiques
En un conjunt ordenat, dit de l’únic element que és més gran que cadascun dels altres elements del conjunt.
límit d’una successió
Matemàtiques
Valor al qual una successió s’acosta més i més (tant com hom vulgui).
Donada una successió { a n }, a 1 ,, a n ,, hom diu que el límit de la successió és A , o que la successió tendeix a a , si per a tot real ε > 0, per petit que sigui, existeix un terme a m de la successió tal que si n > m aleshores | A-a n |
límit d’una funció en un punt
Matemàtiques
Valor al qual tendeix la variable dependent de la funció quan la variable independent tendeix al valor del punt en qüestió.
Donada una funció fD ⊂ ℝ → ℝ i un punt del seu domini de definició, a ∈ D , hom diu que el límit de f quan x tendeix a a és λ, o que f tendeix a λ quan x tendeix a a , si per a tot real ε> 0, per petit que sigui, existeix un real δ> 0 tal que si | x-a | 0 tal que si | x - a | A
combinació amb repetició
Matemàtiques
Tipus de combinació
en què cada element pot repetir-se qualsevol nombre de vegades en una mateixa combinació.
El nombre de combinacions amb repetició d’ordre n , formades a partir d’un conjunt amb m elements, és representat per l’expressió
filera
Matemàtiques
Cadascun dels conjunts d’elements d’una matriu que són disposats en línia recta.
Les fileres horitzontals són anomenades files , i les verticals, columnes
endomorfisme
Matemàtiques
Aplicació d’una certa estructura algèbrica E en ella mateixa, conservant-la.
Hom pot demostrar que el conjunt d’endomorfismes sobre una mateixa estructura té l’estructura d’espai vectorial si hom defineix la suma i el producte d’endomorfismes d’altra banda, llur conjunt adquireix l’estructura d’anell, el qual és isomorf al de les matrius quadrades d’ordre n , atès que cada endomorfisme pot ésser caracteritzat per una matriu Definida una funció determinant no degenerada a E , hom anomena determinant d’un endomorfisme el determinant de la matriu que el representa referida a qualsevol base També pot éser demostrat que el determinant del producte de dos endomorfismes és…
discriminant
Matemàtiques
Invariant funcional que dóna una relació entre els coeficients d’un polinomi i que permet d’estudiar-ne les arrels i d’altres propietats.
En el cas d’un polinomi de grau n amb una sola variable, a 0 x n + a 1 x n - 1 + + a n , el discriminant és l’expressió En particular, el discriminant d’una equació quadràtica ax 2 + bx + c = 0 té com a expressió Δ = b 2 — 4 ac si Δ > 0, l’equació té dues arrels reals diferents, si Δ=0, té dues arrels reals iguals, i si Δ < 0, no té arrels reals sinó complexes
discontinuïtat
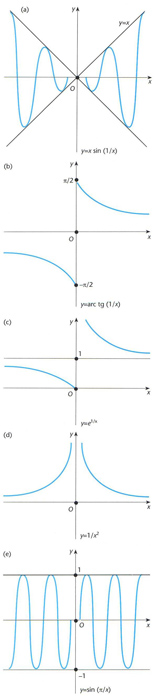
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi aleshores, a és una…