Resultats de la cerca
Es mostren 397 resultats
Roy George Douglas Allen
Economia
Matemàtiques
Economista i estadístic britànic.
Graduat en matemàtiques a Cambridge el 1927, l’any següent s’incorporà a la London School of Econòmics, on desenvolupà tota la seva carrera com a professor d’estadística fins a la jubilació 1973 Fou un pioner en l’aplicació de models matemàtics a l’estudi de l’economia D’entre les seves contribucions destaca A Reconsideration of the Theory of Value 1934, amb J Hicks, i Family Expenditure 1935, amb AL Bowley És conegut també pels seus múltiples manuals sobre economia matemàtica, entre els quals destaquen Mathematical Analysis for Economists 1938, Mathematical Economics 1956 i Macro-Economic…
paraboloide hiperbòlic
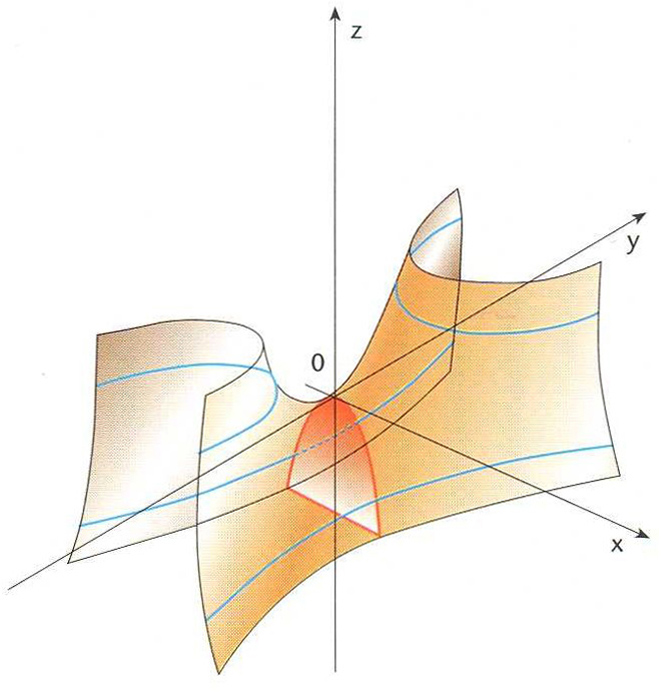
Paraboloide hiperbòlic on hi ha traçada una paràbola i dues hipèrboles
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
—
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola i la intersecció amb un pla perpendicular a l’anterior és una hipèrbola
paraboloide el·líptic
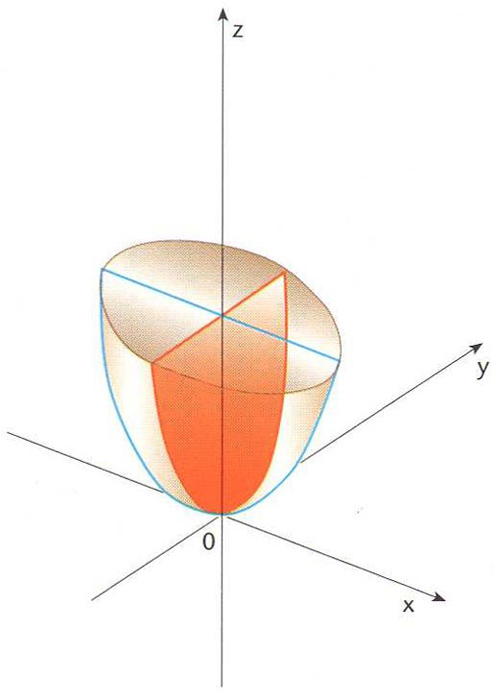
Paraboloide el·líptic on hi ha traçada una el·lipse i una paràbola
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
+
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola, mentre que la intersecció amb un pla perpendicular a l’anterior dóna una ellipse
fracció contínua
Matemàtiques
Expressió de la forma
on l’algorisme s’estén indefinidament.
Hom l’expressa abreujadament mitjançant la notació a 0 + a 1 / b 1 + a 2 / b 2 + a 3 / b 3 + Són emprades per a representar nombres irracionals Així, si α 0 és un nombre irracional positiu, i n ≥0, α 0 admet l’expressió on u n és la part entera de α i α n ≥1 és definit per la relació de recurrència α n - 1 = u n - 1 + 1/α n , n≥1 La successió u n n ≥ 0 és el desenvolupament de α 0 en fracció contínua , i els coeficients u n són els quocients incomplets de la fracció contínua Un exemple d’aquest tipus de desenvolupament és el del nombre π/4, fet per William Brouncker
sèrie de funcions
Matemàtiques
Successió de funcions {
F n
} amb
, on les
f i
són també funcions.
Hom la indica per Σ f n Si { F n } té per límit una funció f , hom diu que la sèrie Σ f n és convergent cap a la funció f i que f és la seva suma, dins el domini on això tingui sentit Si les f i són funcions potencials, f i x = a i x i , la sèrie Σ f n és anomenada sèrie de potències Si la variable x és complexa hom pot demostrar que hi ha un nombre positiu R tal que per a tot x tal que | x | < R la sèrie numèrica Σ a n x n és absolutament convergent, mentre que per a tot x tal que | x | > R la sèrie numèrica Σ a n x n és divergent R és anomenat aleshores radi de convergència de la…
equació integral
Matemàtiques
Equació on la funció que cal determinar es troba dins l’integrant d’una certa integral coneguda.
L’exemple més simple és l’equació , on la funció f x és coneguda i cal trobar la funció f x En virtut del teorema fonamental del càlcul, la solució és, en certes condicions de regularitat, Aquestes equacions les trobem en la resolució matemàtica de problemes físics i tècnics
funció cosinus hiperbòlic complex
Matemàtiques
Funció ch: ℂ→ℂdefinida per l’assignació z →(ez + e-z)/2, on ez és la funció exponencial complexa.
Se satisfà que ch z = cos iz i que cos z = ch iz , on cos és la funció cosinus complex
funció sinus hiperbòlic complex
Matemàtiques
Funció sh: ℂ→ℂdefinida per l’assignació z → (ez-e-z)/2, on ez és la funció exponencial complexa.
Se satisfà que sh z = -i sin iz i que sin z = 1/ i ch iz , on sin és la funció sinus complex
combinació
Matemàtiques
Configuració on hom només té en compte la distinció entre els elements agrupats i no l’ordre en què són presos.
Hom anomena combinació d’ordre n , formada a partir d’un conjunt de m elements 0 ≤ n≤ m, qualsevol dels subconjunts formats en considerar n elements diferents entre els m que integren el conjunt donat, sense tenir-ne en compte l’ordre hom considera, doncs, que dues combinacions són distintes quan algun de llurs elements és diferent El nombre de combinacions d’ordre n , formades a partir d’un conjunt amb m elements, és donat per l’expressió on V n m indica el nombre de variacions, i P n el de permutacions Hom representa sovint C n m per n m , parlant, en aquest, cas, de nombres…
residu d’una funció complexa f (z) analítica en un punt singular A aïllat
Matemàtiques
Quantitat R(f,A) = (1/2πi) ∫cf(z)dz, on C és una corba simple rectificable que envolta A en un entorn de A.
El valor del residu és igual a a-1 , on a-1 és el coeficient del terme 1/ z-A en el desenvolupament infinit de Laurent de f z en un entorn de A
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina