Resultats de la cerca
Es mostren 718 resultats
projectar un punt (una figura) sobre una superfície plana (cilíndrica o cònica)
Matemàtiques
Determinar la intersecció amb una superfície de la recta o de la sèrie de rectes traçades en una direcció determinada des d’un punt o els diferents punts d’una figura.
Johannes de Sacrobosco
Astronomia
Matemàtiques
Nom llatinitzat de l’astrònom i matemàtic anglès John of Holywood
.
És autor d’un tractat d’aritmètica De Algorismo i d’altres obres de tipus didàctic De computo La seva obra més important és, però, De sphaera , resum d’astronomia en quatre capítols, en el qual recull les doctrines de Ptolemeu i d’al-Farġānī, bé que les supera considerablement Aquest text, que estigué en ús a les universitats europees fins a la fi del s XVI, fou comentat per diversos autors posteriors, entre els quals Johann Müller i Philipp Melanchthon
homotècia
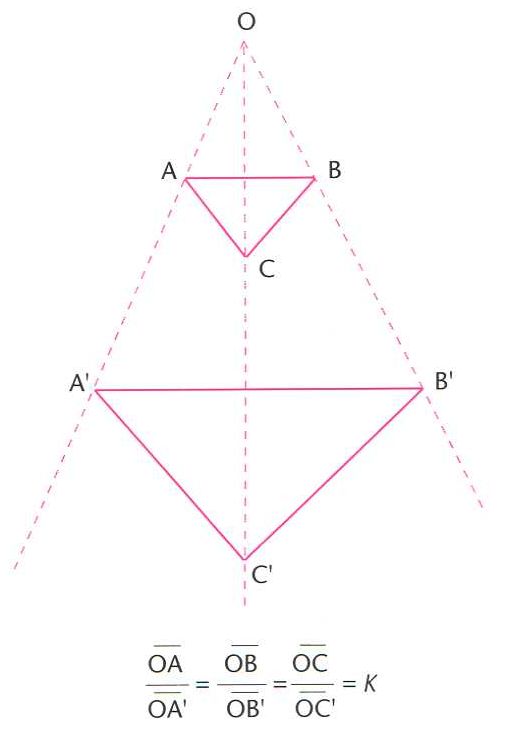
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
Aristòtil

Còpia romana d’Aristòtil del període imperial (segle I o II dC) d’un bronze perdut realitzat per Lísip (Museu del Louvre)
Yuxuan Wang (CC BY-NC-ND 2.0)
Filosofia
Matemàtiques
Filòsof i científic grec, un dels esperits més potents i influents de la història.
Vida i obra Del clan dels asclepíades, era fill de Nicòmac, metge i amic d’Amintes II de Macedònia A divuit anys ingressà a l’Acadèmia Els primers temps fou el deixeble predilecte de Plató, però les divergències posteriors els distanciaren A la mort del mestre 347, Aristòtil abandonà Atenes i passà tres anys a Assos, on s’uní amb Herpillis, de la qual tingué un fill, Nicòmac, al qual dedicà un dels tractats d’ètica D’Assos passà a Mitilene d’aquesta època daten molts dels seus treballs de biologia En 343-342 aC Filip de Macedònia li encarregà l’educació d’Alexandre Aristòtil, que atribuïa una…
abscissa
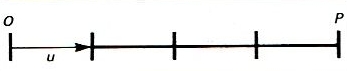
L’abcissa del punt P respecte a l’origen O, amb la unitat u, és 4
Matemàtiques
Fent referència a un punt sobre una recta, distància mesurada amb la unitat adoptada des d’un punt fixat per endavant, anomenat origen, fins al punt considerat.
model
Matemàtiques
Teoria o descripció matemàtica d’un objecte o fenomen real.
L’estudi d’un mateix fenomen real segons diferents criteris permet d’estudiar aquest fenomen mitjançant diferents models matemàtics Creat un o diversos models d’un fenomen, cal recórrer al problema de la verificació o adequació entre el model i la realitat observada Així, per exemple, la teoria de la probabilitat dóna un model dels fenòmens anomenats aleatoris o estocàstics En lògica, un model d’una teoria T és una estructura del llenguatge L T de primer ordre de la mateixa teoria, en la qual estructura tots els axiomes de la teoria tenen valor
integrador
Electrònica i informàtica
Matemàtiques
Tecnologia
Aparell o dispositiu, mecànic o electrònic, destinat al càlcul d’integrals.
Els mecànics poden ésser intègrafs intègraf o integròmetres integròmetre Els integradors electrònics poden efectuar la integració directament sobre un senyal analògic mitjançant amplificadors operacionals, bé que pel mostreig d’un senyal digital i el seu processament mitjançant circuits integrats o bé mitjançant un programa que calculi la funció integral
homologia
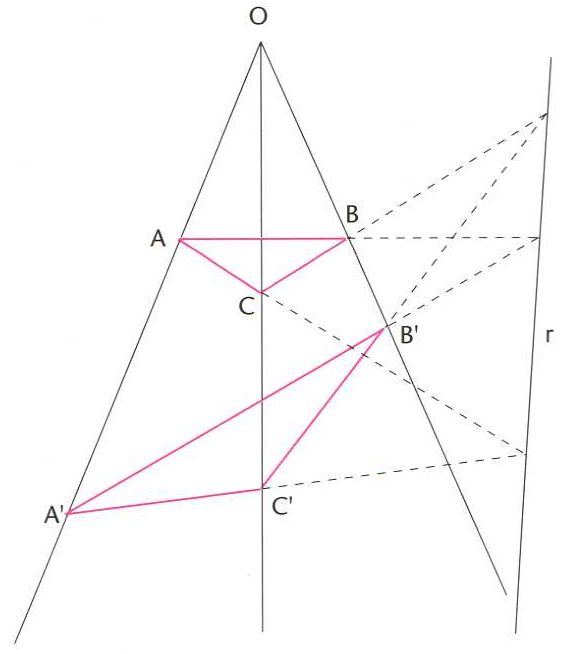
Trasformació per homologia d’un triangle ABC en A'B'C’ (O, centre de l’homologia; r, eix de l’homologia)
© Fototeca.cat
Matemàtiques
Teoria que estudia les transformacions entre espais topològics que conserven certes estructures algèbriques definides en cada espai.
símbol
Matemàtiques
Lletra o signe gràfic de qualsevol mena utilitzat per a representar quantitats (nombres), relacions o operacions.
Cal distingir sempre el símbol del concepte Així, el nombre dos concepte pot ésser representat per símbols diferents 2, II, ╫, etc Principals símbols símbols emprats en teoria de conjunts ∈ pertany a ∉ no pertany a = igual a ≠ diferent ⊂ inclusió, és inclòs en ⊄ no és inclòs en ⋂ intersecció ⋃ reunió − diferència ∁ , − , ∽ complementari ∆ diferència simètrica → aplicació, funció ≃ coordinable, bijectiu x producte cartesià {} singletons claudàtors ∅ conjunt buit ℕ nombres naturals ℤ nombres enters ℚ nombres racionals ℝ nombres reals ℂ nombres complexos símbols emprats en lògica…
catenària
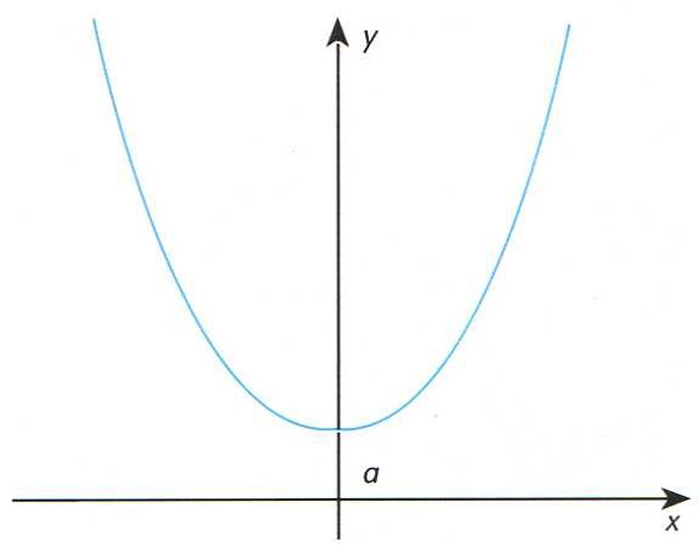
La major o menor concavitat de la corba depèn de la separació dels punts extrems (que es determinen pel paràmetre a de la seva equació)
© fototeca.cat
Matemàtiques
Corba que adopta una cadena, corda, etc, perfectament flexible i amb una càrrega uniformement repartida en tota la seva llargària, fixa en els seus extrems i suspesa lliurement.
L’expressió matemàtica d’aquesta corba és donada per l’equació y=achx/a , on a és la distància des del punt més baix de la corba a l’eix d’abcisses de referència
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina