Resultats de la cerca
Es mostren 4 resultats
rodolament
Matemàtiques
Desplaçament d’una corba, anomenada rodolant, sobre una altra corba fixa, anomenada base, de manera que ambdues restin constantment tangents i que el punt de contacte recorri alhora arcs iguals sobre les dues corbes.
La trajectòria descrita per un punt de la corba mòbil és anomenada ruleta
hipocicloide
Matemàtiques
Corba engendrada per un punt fix d’una circumferència que roda, sense lliscar, per dins d’una altra, mantenint-se ambdues tangents interiors.
La seva equació és on r és el radi de la circumferència fixa, i a , el radi de la circumferència mòbil L’equació s’obté, doncs, de la de l'epicicloide fen a negativa Quan r= 3 a és una deltoide i quan r= 4 a és una astroide
epicicloide
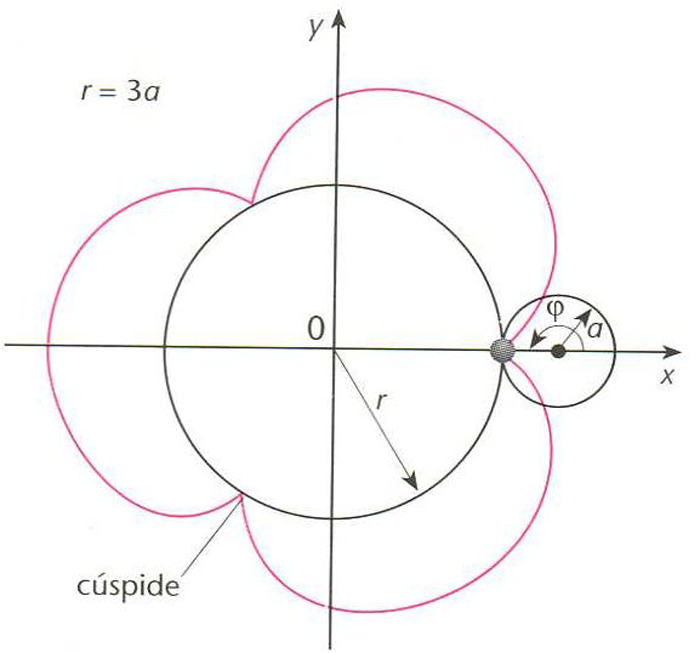
Epiciloide
© fototeca.cat
Matemàtiques
Corba descrita per un punt d’una circumferència que roda sense lliscar sobre una altra, mantenint-se tangents exteriorment ( cicloide
).
La seva equació és on r és el radi de la circumferència fixa, i a , el radi de la circumferència mòbil Si r = na , l’epicidoide té n cúspides n , nombre natural Si r = a la corba degenera en una cardioide Si r= 2 a , ho fa en una nefroide
Mikhail Vasil’jevič Ostrogradskij
Matemàtiques
Matemàtic ucraïnès.
En el camp de la física matemàtica contribuí a resoldre problemes suscitats per la mecànica newtoniana principi d’Ostrogradskij-Hamilton, estudià les deformacions dels cossos elàstics, el desplaçament d’un mòbil dins un medi resistent, etc Establí també una fórmula general que porta el seu nom i permet de passar d’una integral de volum a una integral de superfície teorema de Gauss