Resultats de la cerca
Es mostren 4 resultats
teorema de Menelau
teorema de Menelau
© fototeca.cat
Matemàtiques
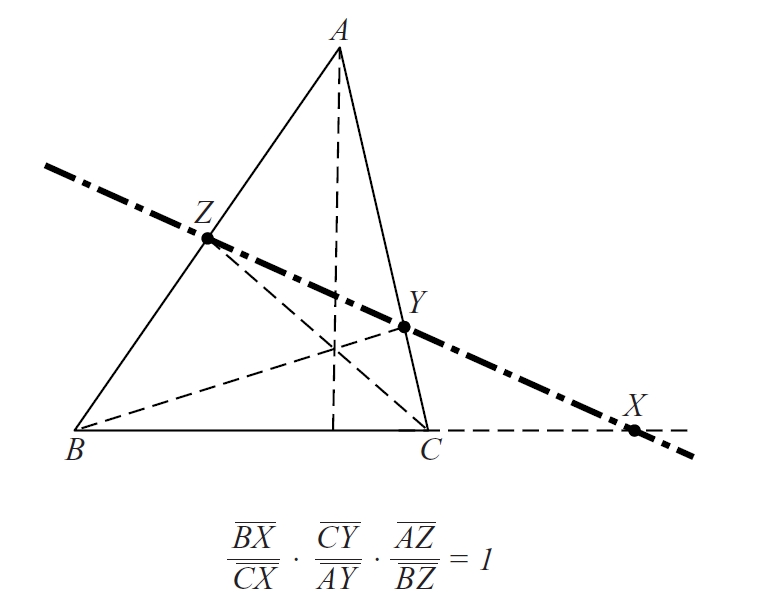
Teorema segons el qual tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB, respectivament, d’un triangle ABC, estan alineats si, i solament si, (BX⁄CX)·(CY⁄AY)·(AZ ⁄ BZ) = 1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui +1 X , A , B Y , B , C Z , C , A = 1 Aquest teorema és dual del teorema de Ceva
Menelau d’Alexandria
Matemàtiques
Matemàtic grec.
Fou el primer a separar la trigonometria de l’estereometria i l’astronomia Féu la primera definició de triangle esfèric i utilitzà la relació entre els triangles esfèrics i els plans per a resoldre els triangles esfèrics teorema de Menelau Escriví el tractat Esfèrica , on establí els fonaments de la trigonometria esfèrica
teorema de Ceva
teorema de Ceva
Matemàtiques
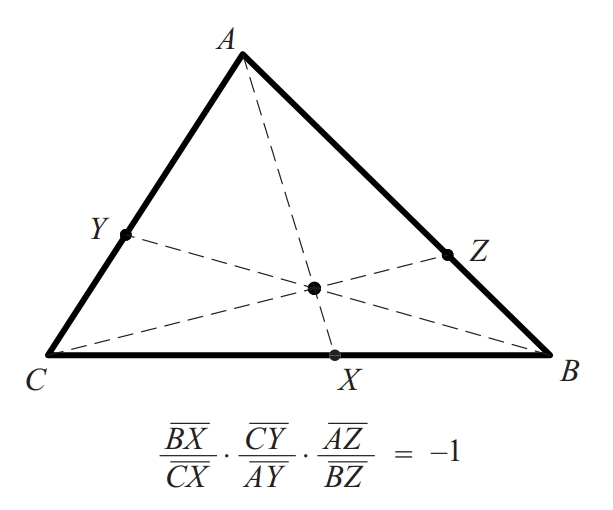
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…