Resultats de la cerca
Es mostren 9 resultats
fórmula de Bayes
Matemàtiques
Fórmula que permet de calcular, donades les probabilitats a priori P (Ai) corresponents a diverses causes A1,..., An, mútuament excloents, les probabilitats a posteriori P (Ai/B).
Aquestes probabilitats aposteriori o condicionades indiquen el fet que la causa A i hagi estat precisament la que ha motivat l’efecte B observat Té com a expressió La impossibilitat de conèixer en molts casos les probabilitats a priori és una limitació pràctica de l’aplicació de la fórmula
Hans Reichenbach
Filosofia
Matemàtiques
Filòsof i matemàtic alemany.
Professor a Berlín des del 1926, fou destacat representant de l’anomenat Grup de Berlín, neopositivista i vinculat al cercle de Viena, i des del 1930 dirigí, amb R Carnap, la revista Erkenntnis des del 1933 professà a Istanbul i des del 1938 a la Universitat de Califòrnia, on es traslladà fugint dels nazis Seguidor, bé que moderat, dels desenvolupaments de l’empirisme lògic, l’empirisme científic i el moviment per a la ciència unificada, és autor de moltes obres sobre la nova imatge física del món i les seves implicacions filosòfiques,…
inferència bayesiana
Biologia
Matemàtiques
Mètode estadístic d’inferència que consisteix a maximitzar la probabilitat posterior d’una hipòtesi determinada.
Recentment s’ha incorporat a l’estimació de filogènies L’arbre filogenètic òptim és aquell que maximitza la probabilitat posterior d’obtenir la hipòtesi La probabilitat posterior és proporcional a la seva màxima probabilitat multiplicada per la probabilitat apriori de la hipòtesi, que consisteix a incorporar els coneixements previs a la realització de l’anàlisi Aquest mètode proporciona directament estimacions de les probabilitats de cada branca de l’arbre filogenètic i incorpora models sobre el procés d’evolució…
demostració
Lògica
Matemàtiques
Derivació d’un enunciat, mitjançant l’aplicació d’unes determinades regles lògiques, a partir d’uns altres enunciats, dits premisses de la demostració.
Qualsevol cadena de demostracions ha d’arrencar d’un conjunt finit de premisses no demostrables, els axiomes Aquest conjunt és anomenat el sistema dels axiomes de la teoria deductiva, i els enunciats que són demostrats a partir dels axiomes s’anomenen teoremes Identificada, en la teoria platònica, amb la definició, Aristòtil la considerà com un procés superior, adreçat a extreure, mitjançant el sillogisme, una conclusió a partir d’unes premisses certes L’escolàstica s’adherí a l’esquema aristotèlic i n'elaborà una classificació propter…
William Kingdon Clifford
Filosofia
Matemàtiques
Matemàtic i filòsof anglès.
A partir d’una generalització dels treballs sobre els quaternions de William Rowan Hamilton, el 1872 introduí un nou tipus de nombres complexos, els biquaternions, que aplicà fonamentalment a l’estudi de les geometries no euclidianes Estudià les estructures topològiques de l’espai i suggerí que la matèria és un tipus particular de curvatura de l’espai, amb la qual cosa prefigurava la teoria de la relativitat general d’Einstein, i explicità les dificultats que les geometries no euclidianes presenten a la teoria de les proposicions sintètiques ‘a…
mesura
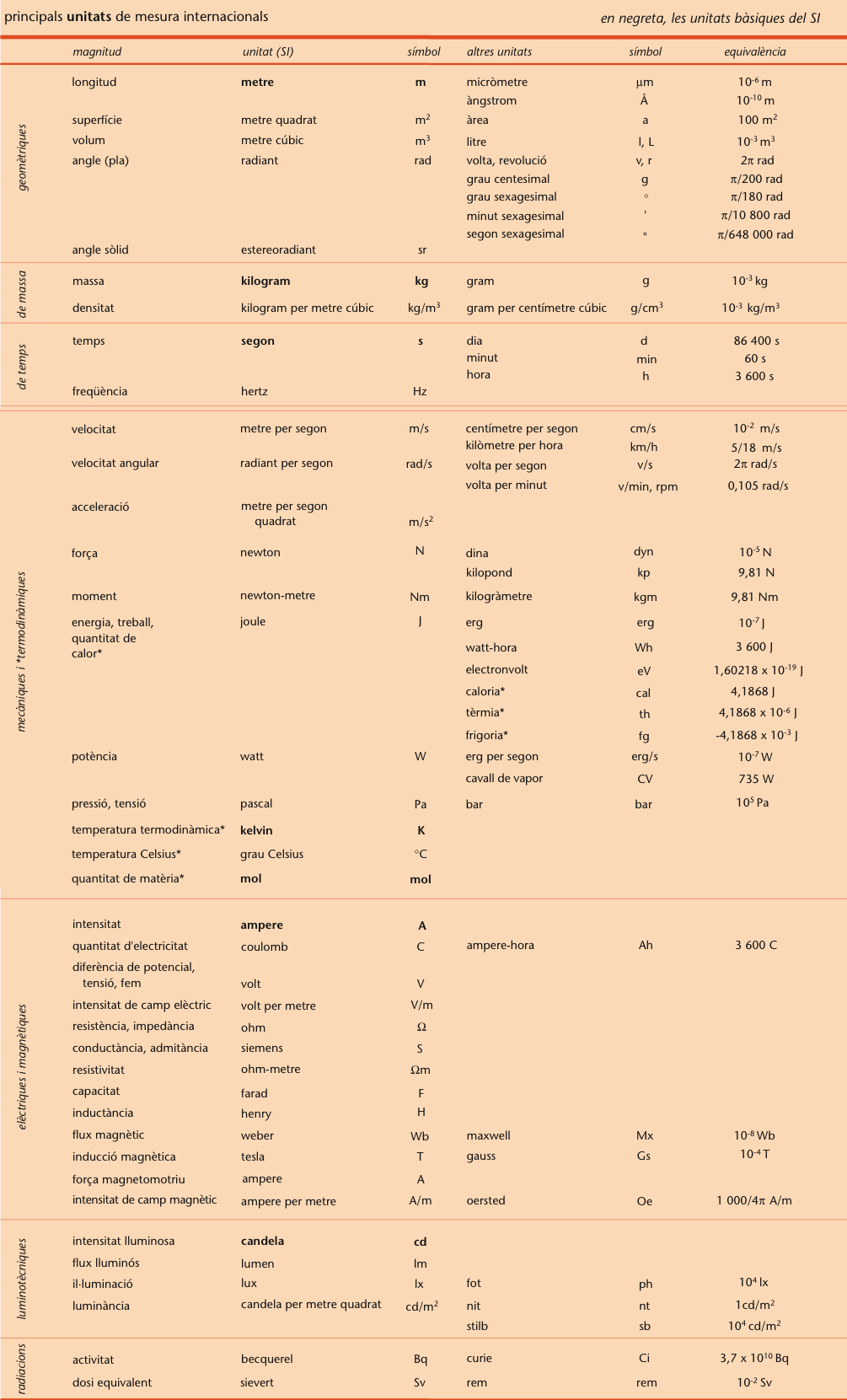
Principals unitats de mesura internacional
© Fototeca.cat
Física
Matemàtiques
Valor numèric obtingut experimentalment com a resultat d’un mesurament consistent a comparar una magnitud amb una altra de la mateixa espècie elegida com a unitat
, amb la finalitat d’establir unes relacions o la deducció d’unes conclusions.
Certes mesures, però, poden ésser de tipus qualitatiu “sí o no”, “més gran que o igual a”, “lineal”, etc, o poden estar relacionades amb una entitat gràfica d’imatge que serà donada per una “concentració” o per una probabilitat obtinguda per repetició del fet experimental El procés de mesura ha d’ésser objectiu i, per tant, la comparació ha d’ésser feta amb una magnitud unitat de la mateixa espècie i de similar dimensió Si hom l’efectua per un procés indirecte transductor, la magnitud final ha d’ésser calibrada en unitats de la magnitud primitiva No totes les magnituds són…
conjectura
Matemàtiques
Hipòtesi emesa a priori
sobre l’exactitud o la inexactitud d’un enunciat del qual hom ignora encara la demostració.
Gottfried Wilhelm Leibniz
Filosofia
Física
Història
Matemàtiques
Història del dret
Filòsof alemany de cultura enciclopèdica, com ho testifiquen les seves aportacions en altres terrenys: matemàtica, física, història, dret i religió.
Conseller de l’elector de Magúncia 1672, fou enviat a París, on residí quatre anys, decisius per a la seva formació Sis anys abans, però, quan aspirava a una plaça de professor de filosofia a Leipzig, ja publicà una Dissertatio de arte combinatoria , inspirada en l' Ars magna de Llull Bibliotecari i historiògraf dels ducs de Hannover, viatjà per tot Alemanya i Itàlia intensificà, així, els seus contactes amb molts savis de l’època També es relacionà amb el cercle lullià de Magúncia i fou amic de Buchels, collaborador de Salzinger en l’edició maguntina de les obres de Llull 1721-42 Entre les…
matemàtica
Matemàtiques
Ciència que estudia les propietats dels nombres, de les figures, dels conjunts, de les operacions, de les funcions, etc.
Aquesta definició és força descriptiva, però incompleta, i per això diversos matemàtics han intentat de definir la matemàtica tot assenyalant-ne els trets més característics Així, segons B Russell, la matemàtica consisteix només en afirmacions tals com “si una proposició és veritable referida a un objecte, aleshores una altra proposició també ho és”, de manera que la matemàtica és aquell camp en què hom no sap mai de què parla ni si allò que diu és veritat o no Dins aquesta mateixa línia, H Poincaré diu que els matemàtics no estudien objectes, sinó relacions entre objectes no els interessa la…