Resultats de la cerca
Es mostren 10 resultats
circumcentre
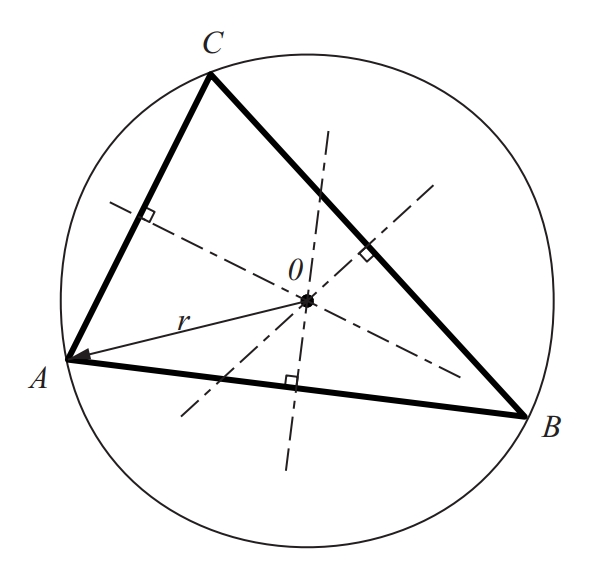
Circumcentre del triangle ABC
Matemàtiques
Centre d’una circumferència que és circumscrita a una figura determinada.
En el cas d’un triangle és la intersecció de les tres mediatrius
homotècia
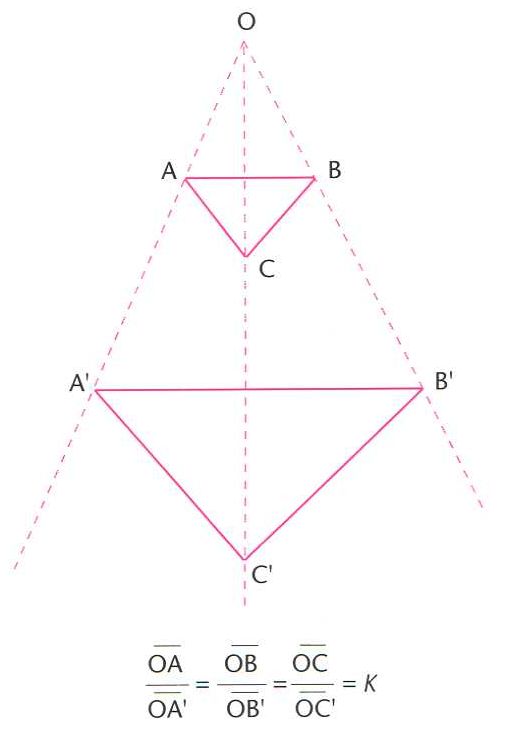
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
homologia
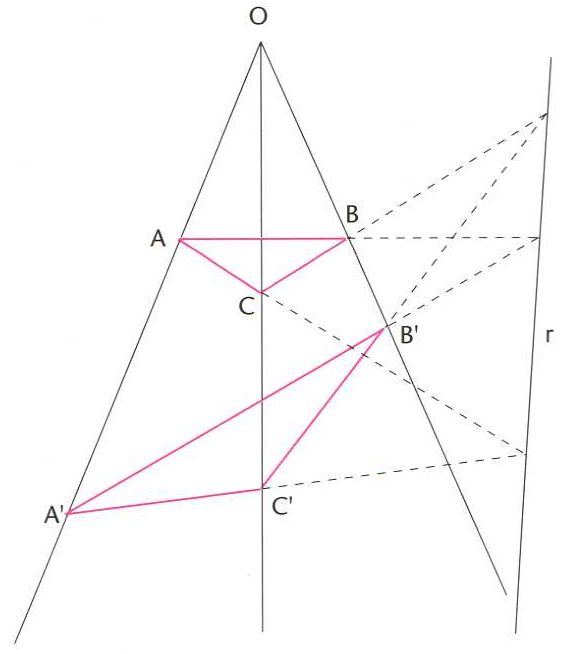
Trasformació per homologia d’un triangle ABC en A'B'C’ (O, centre de l’homologia; r, eix de l’homologia)
© Fototeca.cat
Matemàtiques
Teoria que estudia les transformacions entre espais topològics que conserven certes estructures algèbriques definides en cada espai.
punt de Fermat
Matemàtiques
Donat un triangle ABC, punt de concurrència F de les rectes AA’, BB’ i CC’ determinades gràcies als triangles equilàters exteriors ABC’, ACB’ i BCA’.
ortòedre
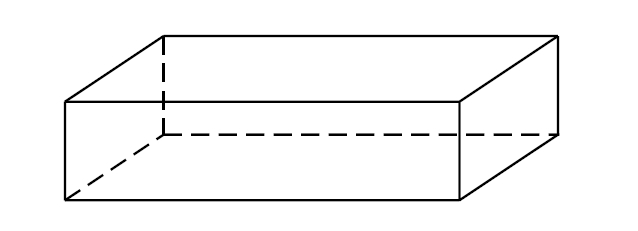
Ortòedre
Matemàtiques
Prisma de sis cares rectangulars que té tots els angles rectes.
Si les longituds de les arestes són a, b i c , la fórmula del volum de l’ortòedre és V=abc
punts de Brocard
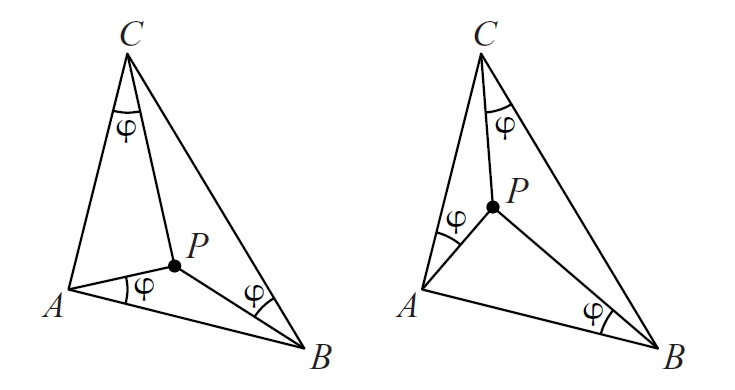
punts de Brocard
© fototeca.cat
Matemàtiques
Punts P d’un triangle ABC tals que els angles PBC, PCA i PAB són iguals.
En tot triangle n’hi ha dos
punt isoperimètric
Matemàtiques
En un triangle ABC, punt interior que determina amb els vèrtexs A, B i C tres triangles isoperimètrics.
És anomenat també punt de Kimberling
problema de Fermat
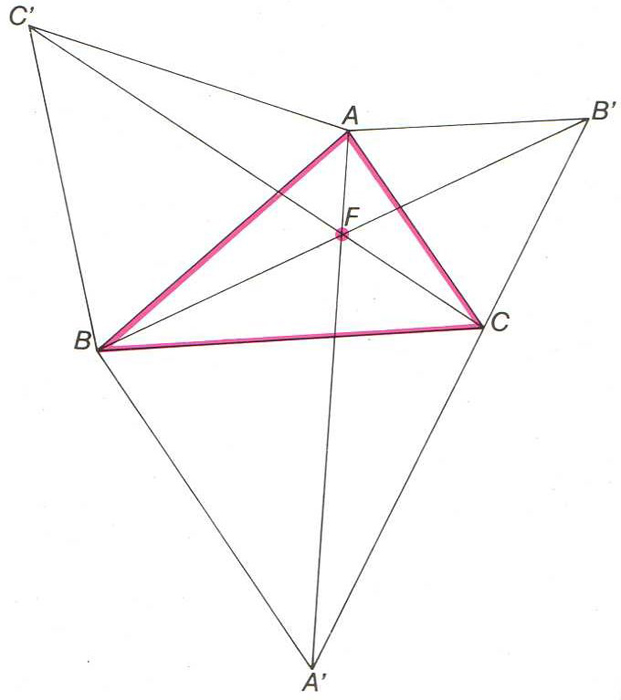
Problema de Fermat
© fototeca.cat
Matemàtiques
Donat un triangle ABC, problema que consisteix a trobar un punt M del pla per al qual la suma MA + MB + MC, és mínima.
El problema admet com a solució el punt de Fermat , si els tres angles del triangle són menors que 120°
teorema de Menelau
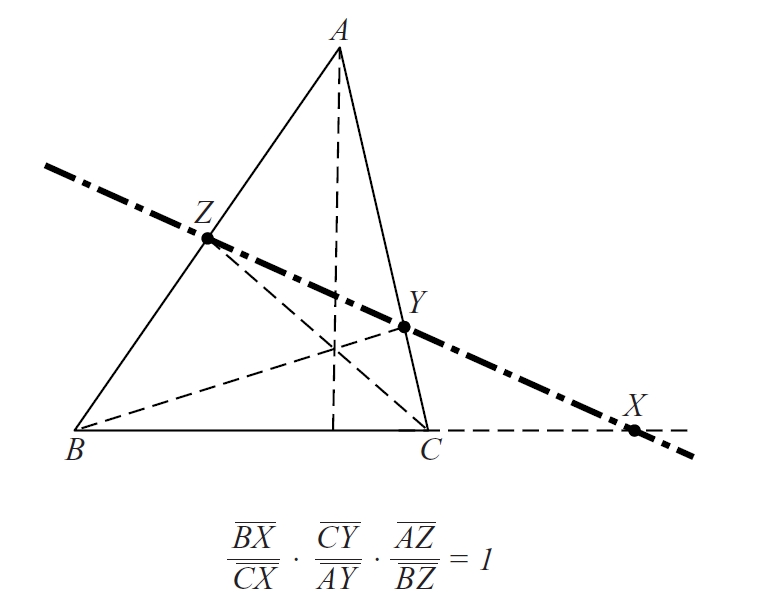
teorema de Menelau
© fototeca.cat
Matemàtiques
Teorema segons el qual tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB, respectivament, d’un triangle ABC, estan alineats si, i solament si, (BX⁄CX)·(CY⁄AY)·(AZ ⁄ BZ) = 1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui +1 X , A , B Y , B , C Z , C , A = 1 Aquest teorema és dual del teorema de Ceva
teorema de Desargues
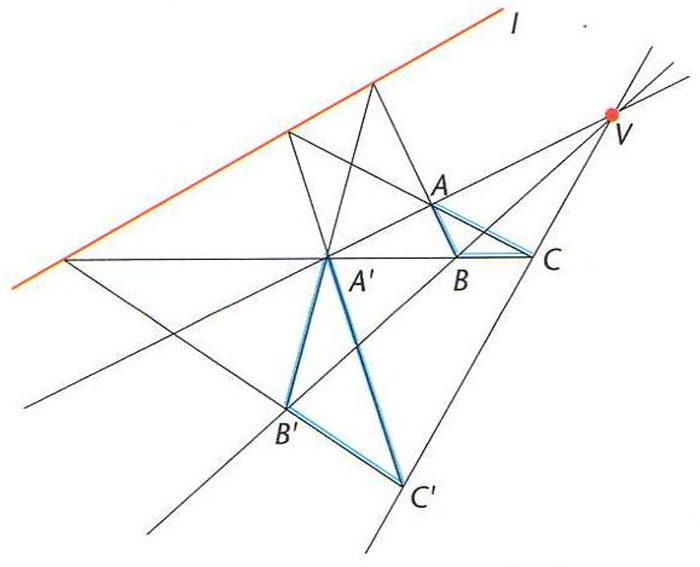
V és el punt de concurrència de les rectes AA’, BB' i CC' i l és la línia que conté els punts de concurrència de AB i A'B', de BC i B'C' i de CA i C'A'
© fototeca.cat
Matemàtiques
Teorema segons el qual, donats dos triangles ABC i A’B’C’ tals que les rectes AA’, BB’ i CC’ són concurrents, els punts de concurrència de AB i A’B’, de BC i B’C’ i de CA i C’A’ són alineats.