Resultats de la cerca
Es mostren 5 resultats
funció additiva
Matemàtiques
Donats dos conjunts dotats de sengles operacions internes notades additivament, (E, +) i (F, +), funció f:E →F que satisfà f(x+y)=f(x)+f(y).
En teoria de nombres, una funció additiva és una funció f ℕ-{0}→ℂtal que f xy = f x + f y quan x i y són nombres primers entre ells
terme
Matemàtiques
Cadascuna de les parts que formen una expressió algèbrica additiva.
Així, en 5 x 2 -3 x+2 hi ha tres termes 5 x 2 , -3 x i +2 En general hom parla de termes algèbrics, trigonomètrics, exponencials, logarítmics , etc, segons que les variables apareguin afectades per les respectives funcions algèbriques polinomis, trigonomètriques sinus, cosinus, tangent, etc
volum
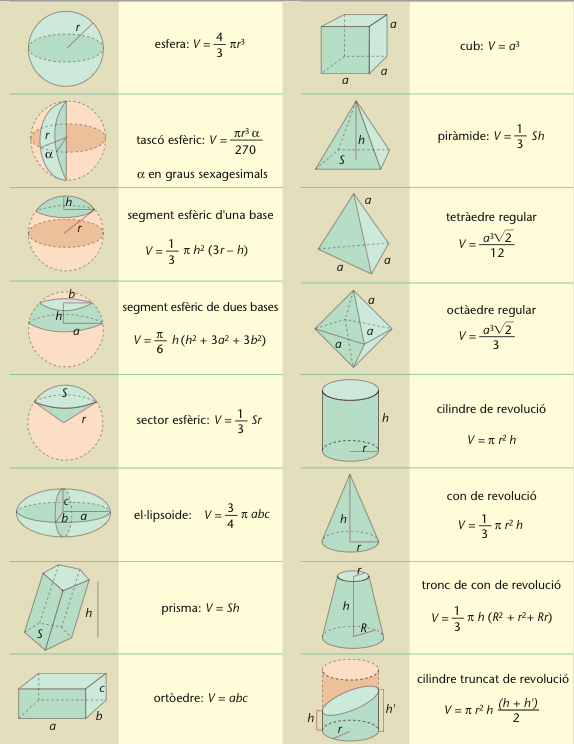
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples…
signe sumatori
Matemàtiques
Signe, representat per la lletra grega Σ, que hom empra per a simplificar una notació additiva, com, per exemple
.
mesura
Matemàtiques
Aplicació m definida entre una àlgebra de conjunts ɑ d’un espai mesurable (Ω, ɑ) i el conjunt ℝ+ dels nombres reals positius.
L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑ és igual a la suma de les respectives mesures, és a dir ∀ A ∈ ɑ i ∀ B ∈ ɑ tals que A ∩ B = ∅, m A + m B La terna Ω, ɑ, m és anomenada espai de mesura , i els conjunts de l’àlgebra ɑ són anomenats mesurables En el cas que ɑ sigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑ disjunts dos a dos és igual a la suma de les respectives mesures, és a dir essent A i ∈ ɑ i A i ∩ A j = ∅, per a tot i, j tals que i ≠ j Una mesura és anomenada fitada…