Resultats de la cerca
Es mostren 4 resultats
paraboloide
Matemàtiques
Superfície de segon grau o quàdrica que, en ésser tallada en qualsevol dels seus punts per un pla adequat, dóna una paràbola.
rotació
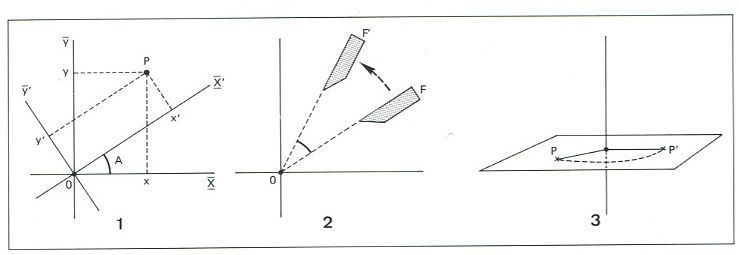
rotació: 1, d'eixos; 2, al voltant d'un punt0; 3, al voltant d'un eix
Matemàtiques
Transformació geomètrica que constitueix un dels moviments rígids del pla o de l’espai i que conserva les distàncies (mides i forma) i l’orientació de les figures sobre les quals és aplicada.
En el pla hom considera la rotació al voltant d’un punt fix que correspon a moviments rígids circulars de centre al punt donat En l’espai hom considera la rotació al voltant d’una línia , en la qual qualsevol punt d’una figura es mou en sentit circular al voltant de la línia donada eix de rotació, en un pla perpendicular a aquesta i que passa pel punt donat Una rotació d’eixos correspon a una rotació que deixa fix l’origen de coordenades Aquestes rotacions permeten de passar d’un sistema de referència a un altre que pot ésser més adequat per a l’estudi d’un problema geomètric…
problema
Matemàtiques
Tota qüestió en què partint d’unes dades conegudes cal arribar a uns resultats.
El resultat d’un problema pot ésser de natura molt diversa cal distingir, dins la matemàtica, els problemes de calcular, els problemes de construir i els problemes de demostrar En els problemes de calcular , és possible que per analogia amb altres problemes ja coneguts hom pugui aplicar unes regles que donen directament la solució, que pot constar d’un o més nombres Quan aquestes regles no són fàcils de descobrir hom recorre a expressar algèbricament les condicions de l’enunciat, és a dir, expressar per mitjà d’equacions les relacions entre les dades i les incògnites del problema…
mesura
Matemàtiques
Aplicació m definida entre una àlgebra de conjunts ɑ d’un espai mesurable (Ω, ɑ) i el conjunt ℝ+ dels nombres reals positius.
L’aplicació compleix que la mesura de la unió de dos conjunts A i B de ɑ és igual a la suma de les respectives mesures, és a dir ∀ A ∈ ɑ i ∀ B ∈ ɑ tals que A ∩ B = ∅, m A + m B La terna Ω, ɑ, m és anomenada espai de mesura , i els conjunts de l’àlgebra ɑ són anomenats mesurables En el cas que ɑ sigui una σ-àlgebra de Borel, una mesura m és anomenada σ-additiva si la mesura d’una unió infinita i numerable de conjunts de ɑ disjunts dos a dos és igual a la suma de les respectives mesures, és a dir essent A i ∈ ɑ i A i ∩ A j = ∅, per a tot i, j tals que i ≠ j Una mesura és anomenada fitada…