Resultats de la cerca
Es mostren 12 resultats
inversió
Matemàtiques
Transformació geomètrica del pla o de l’espai que, donat un punt O
, anomenat centre d’inversió
, i un nombre k
, anomenat potència
, fa correspondre a cada punt P
un altre punt P´
.
De manera que O, P i P' són alineats, i els segments compleixen la relació La inversió és una transformació isogonal
homotècia
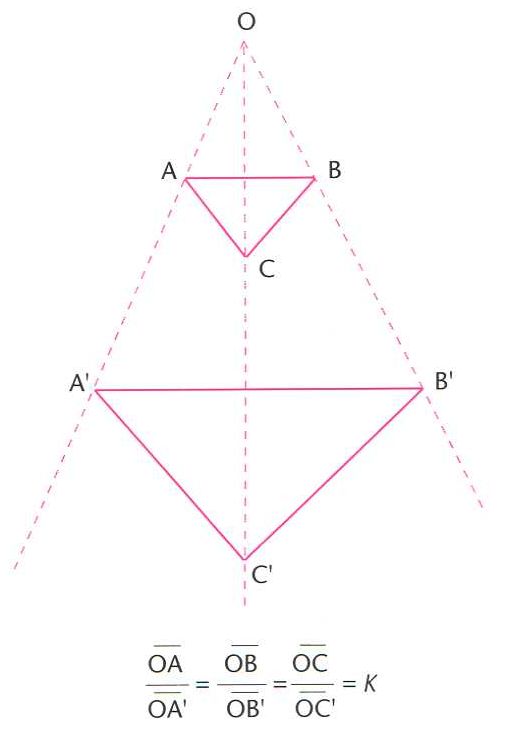
Homotècia, transformació homotètica d’un triangle ABC (O, centre de l’homotècia; k, raó d’homotècia)
© Fototeca.cat
Matemàtiques
Transformació geomètrica del pla o de l’espai que compleix aquestes dues condicions.
Qualsevol punt A i la seva imatge A' són alineats amb un punt fix O anomenat centre d’homotècia , i els segments compleixen la relació k essent, per a cada homotècia, una constant real anomenada raó de l’homotècia Les homotècies transformen rectes en rectes, circumferències en circumferències i conserven els angles
espai projectiu
Matemàtiques
Conjunt de classes d’equivalència, P, de punts de Rn + 1 — {Ō}.
On R n + 1 és un espai vectorial de dimensió n + 1, obtingudes per la relació ''dos punts x i x' estan relacionats si i només si estan alineats amb l’origen’, és a dir, si es verifica x ' 1 ,, x' n + 1 = r x 1 ,, x n 1 per a tot nombre real r ≠ 0 El seu estudi pertany a la geometria projectiva
raó simple
Matemàtiques
Donats tres punts alineats A, B i C, relació
.
La raó simple és un invariant en una projecció
raó doble
Matemàtiques
Donats quatre punts alineats A, B, C i D, relació
.
La raó doble és un invariant en una projecció
triangle
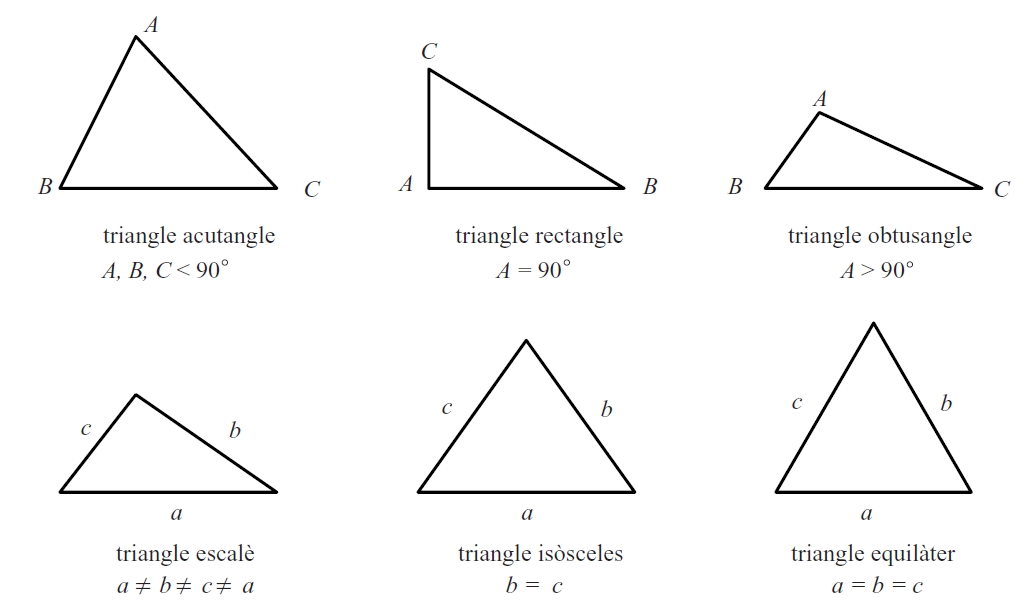
triangles
Matemàtiques
Figura formada en unir tres punts (anomenats vèrtexs) no alineats amb tres segments de línia recta.
Un triangle és anomenat acutangle si els seus angles interiors són aguts, obtusangle si té un angle interior obtús, escalè si cap costat és igual als altres dos, isòsceles si té dos costats iguals, equilàter si té tots tres costats iguals, i rectangle si un dels angles interiors és un angle recte 90° Si no és rectangle és anomenat obliquangle L’àrea d’un triangle és igual a la meitat del producte de la base qualsevol costat per l’altura recta perpendicular des del vèrtex oposat a la base fins a aquesta base La resolució d’un triangle , és a dir, la determinació dels seus angles i costats, a…
homologia
Matemàtiques
Transformació geomètrica del pla o de l’espai tal que cada punt i la seva imatge són alineats amb un punt fix anomenat centre d’homologia, i si tres punts són alineats, llurs imatges també ho són.
pla

Equació del pla
© fototeca.cat
Matemàtiques
Superfície tal que qualsevol recta que passi per dos dels seus punts es troba totalment continguda en la dita superfície.
Els plans, juntament amb els punts i les rectes, són els elements geomètrics primitius en l’axiomatització de Hilbert de la geometria D’altra banda, un pla és determinat per tres punts no alineats, o bé per dues rectes que es tallin o siguin paralleles, o bé per un punt i una recta que no contingui el punt A l’espai euclidià ℝ 3 un pla pot ésser representat per l’equació A x— x 1 + B y— y 1 + C z— z 1 = 0, en la qual x 1 , y 1 , z 1 són les tres coordenades d’un punt P 1 donat del pla, A, B, C són les tres components d’un vector N normal al pla, i x, y, z són les tres…
teorema de la recta d’Euler
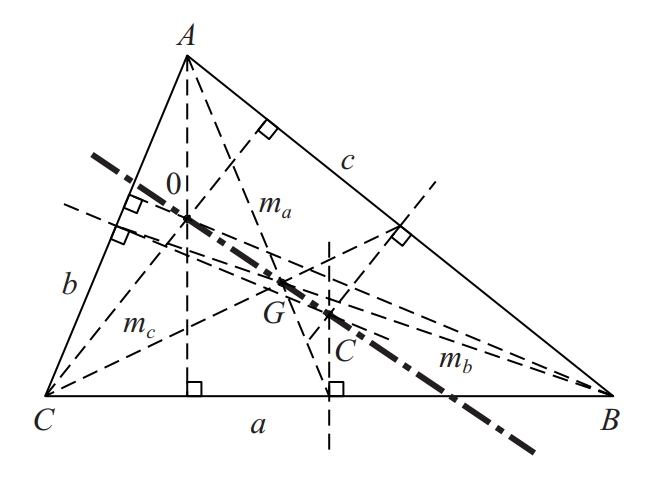
teorema de la recta d’Euler
Matemàtiques
Resultat que prova que l’ortocentre, el circumcentre i el baricentre d’un triangle estan alineats i que el baricentre és a una distància doble de l’ortocentre que del circumcentre.
La recta que passa per aquests punts s’anomena recta d’Euler
teorema de l’hexàgon de Pappus
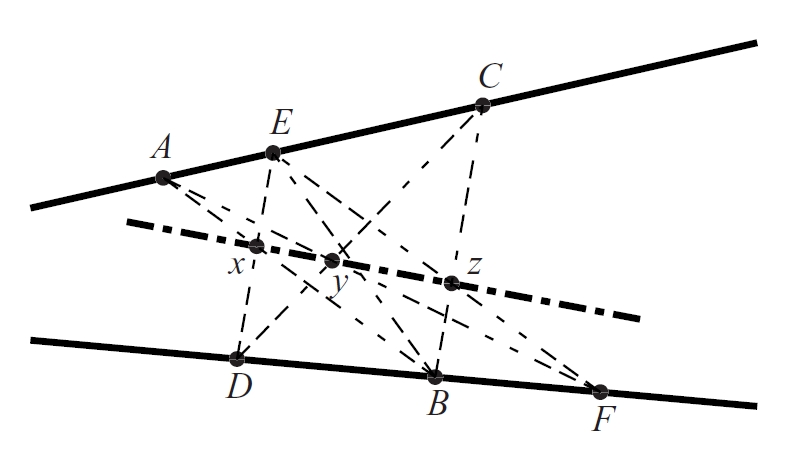
teorema de l’hexàgon de Pappus
Matemàtiques
Teorema segons el qual, si els sis vèrtexs d’un hexàgon estan alternativament sobre dues rectes, aleshores els tres parells de costats oposats (si cal, prolongats) es tallen en tres punts que estan alineats.