Resultats de la cerca
Es mostren 18 resultats
altura
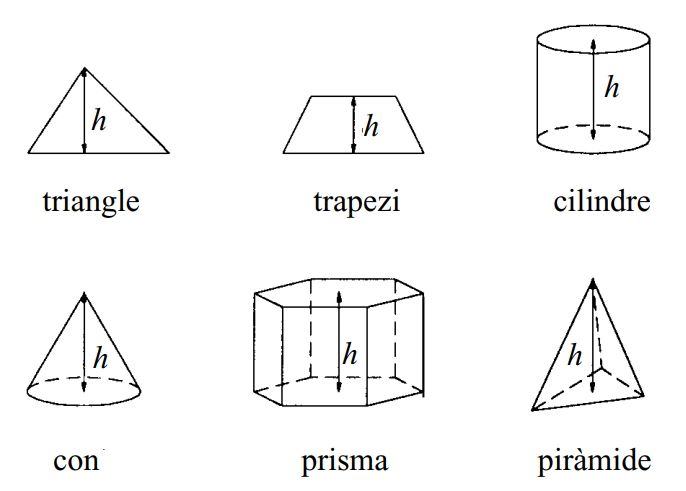
Altures de diferents figures i cossos geomètrics
© Fototeca.cat
Matemàtiques
Segment de recta (o també la seva longitud) en les figures i en els cossos geomètrics comprès entre dos de llurs elements (un vèrtex i un costat al triangle, dos costats al paral·lelogram) i perpendicular almenys a un d’aquests elements, anomenat base, o bé a una recta o a un pla que els determini.
Moltes figures i molts cossos presenten diverses altures segons quin costat hom prengui com a base En un triangle, les tres altures es tallen en un punt dit ortocentre i els seus peus determinen el triangle òrtic
gràfic
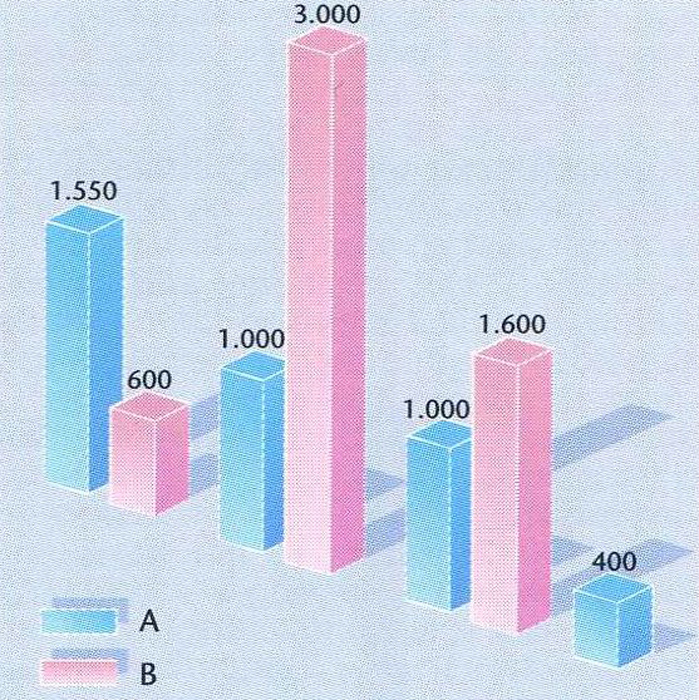
Gràfic de barres. L’altura de les barres és proporcional a la magnitud representada a l’eix de les ordenades
© fototeca.cat
Matemàtiques
Dibuix representatiu d’un conjunt de dades estadístiques.
Gràfic en espiral El valor, en cada mes, de la magnitud representada és proporcional a la distància al centre del corresponent punt de referència © fototecacat Gràfic lineal Aquest tipus de representació permet de comparar diverses sèries de dades © fototecacat Gràfic sectorial L’àrea de cada sector és proporcional al valor de la dada representada © fototecacat Gràfic simbòlic les dades a representar són proporcionals al nombre de figuires de cada línia © fototecacat
zona

Zona esfèrica
© Fototeca.cat
Matemàtiques
Porció de superfície esfèrica compresa entre les dues interseccions de dos plans paral·lels amb l’esfera.
L’altura d’una zona esfèrica és la distància perpendicular entre els dos plans que la determinen, i la seva àrea val 2π Rh , on R és el radi de l’esfera i h l’altura de la zona
trapezi
Matemàtiques
Quadrilàter que té dos costats oposats paral·lels i els altres dos no paral·lels.
Els dos costats parallels b 1 i b 2 són les bases , i llur distància h és l' altura del trapezi L’àrea és h b 1 + b 2 /2, és a dir, el producte de l’altura per la semisuma de les bases Si els costats no parallels són iguals, és anomenat trapezi isòsceles
piràmide
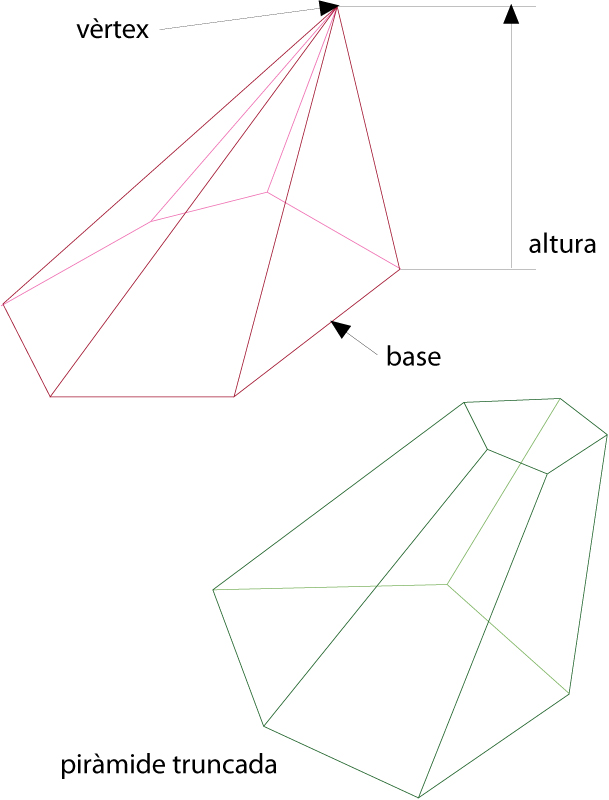
Piràmide irregular de base hexagonal i piràmide truncada de base pentagonal
© Fototeca.cat
Matemàtiques
Políedre que té per base un polígon qualsevol i les altres cares del qual (anomenades cares de la piràmide) són triangles que tenen un vèrtex comú (anomenat vèrtex de la piràmide).
Una piràmide és anomenada triangular tetràedre, quadrangular, pentagonal , etc, segons que la base sigui, respectivament, un triangle, un quadrilàter, un pentàgon, etc Una piràmide és anomenada regular si la base és un polígon regular i les cares són triangles isòsceles Hom anomena altura d’una piràmide la distància del vèrtex al pla del polígon El volum de la piràmide és el terç de la superfície de la base per l’altura Tallant una piràmide amb un pla hom obté dos políedres El políedre que conté el vèrtex és també una piràmide L’altre rep el nom de piràmide truncada
con
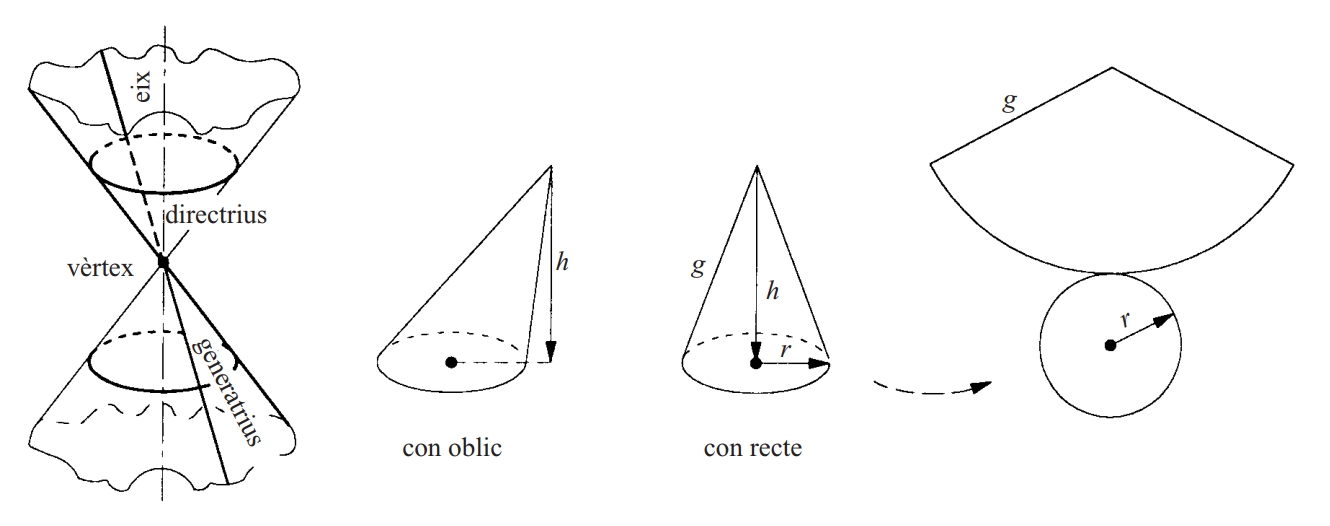
con
© Fototeca.cat
Matemàtiques
Cos limitat per un pla que conté una corba tancada (base del con) i pel conjunt de semirectes que, partint d’un punt fix (vèrtex del con) exterior al pla de la base, recolzen sobre la corba.
Es parla de con circula r si la base és una circumferència En un con circular, si la projecció del vèrtex sobre el pla de la base coincideix amb el centre, es parla de con recte , en cas contrari es parla de con oblic Els segments que tenen per extrems el vèrtex i un punt qualsevol de la base s’anomenen generatrius l’altura d’un con és la distància del vèrtex al pla de la base El volum d’un con és un terç de l’àrea de la base per l’altura L’àrea lateral d’un con circular recte és π rg , essent r el radi de la base i g la longitud de la generatriu
apotema
Matemàtiques
Altura de qualsevol de les cares laterals d’una piràmide regular.
histograma
Matemàtiques
Representació gràfica, formada per rectangles, de les freqüències d’una variable.
Quan la variable pren valors discrets, tots els rectangles tenen la mateixa amplada i llur altura és proporcional a la freqüència corresponent al punt on el rectangle és situat Quan la variable és contínua, els rectangles són contigus i l’àrea de cadascun d’ells, que té per base un cert interval de la variable, és proporcional al valor global de la freqüència corresponent a l’interval