Resultats de la cerca
Es mostren 14 resultats
corbes de Lissajous
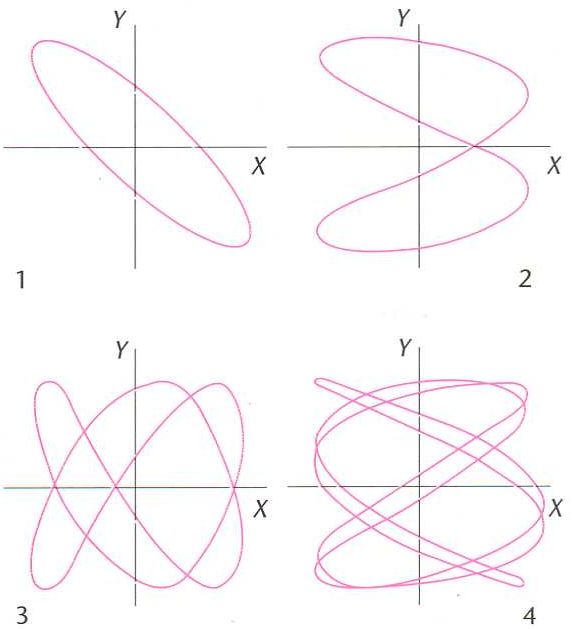
Corbes de Lissajous la relació entre les pulsacions wx i wy dels dos moviments corresponents.
© Fototeca.cat
Matemàtiques
Corbes que apareixen en la composició de dos moviments vibratoris harmònics perpendiculars entre ells.
Hom obté corbes molt diverses, en general obertes, però, si la relació entre els períodes dels dos moviments és racional, la corba obtinguda és tancada i el moviment resultant és periòdic si els dos períodes són iguals, la corba resultant és una circumferència o una ellipse Hom les pot reproduir fàcilment en un oscilloscopi fent que les tensions horitzontal i vertical siguin sinusoidals
terme
Matemàtiques
Cadascuna de les parts que apareixen a l’esquerra o a la dreta d’una igualtat o desigualtat.
equació diferencial
Matemàtiques
Equació funcional (en el sentit que les incògnites són funcions) on apareixen les derivades de la funció incògnita.
Si la funció és d’una sola variable, l’equació és una equació diferencial ordinària Per tal que aquesta definició, molt general, no inclogui certes classes d’equacions especials com és ara les equacions diferencials en diferències f ´ x = f x + h , hom precisa que la funció incògnita i les seves derivades tan sols poden ésser sotmeses a operacions algèbriques El tipus general d’equació diferencial és escrit F t,x,x´,,x n = 0 Hom defineix l' ordre d’una equació diferencial com el de la màxima derivada que apareix en l’equació Si F té forma polinòmica, hom parla de grau de l’equació…
nombres de Bernoulli
Matemàtiques
Nombres racionals Bn que apareixen com a coeficients dels termes, per a n parell de la forma
en el desenvolupament en sèrie de potències de la funció Així, B 1 = 1/6, B 2 = -1/30, B 3 = 1/42, etc Alguns autors anomenen nombres de Bernoulli els coeficients B n de x n / n en el desenvolupament de MacLaurin de x / e x -1, de què resulta B 0 = 1, B 1 = -1/2, B 2 = 1/6, B 4 = -1/30, B 6 =1/92, … i B 2 n +1 =0 Hom empra els nombres de Bernoulli en fórmules d' integració numèrica i en càlcul de diferències finites
Elwin Bruno Christoffel
Matemàtiques
Matemàtic alemany.
Treballà especialment en el camp de la geometria diferencial Introduí els símbols que duen el seu nom símbols de Christoffel associats a la forma quadràtica gμν, símbols que apareixen en la relativitat general
atracció
Matemàtiques
Fenomen segons el qual uns ens determinats (punts, rectes, nombres, etc.) passen a tenir una funció especial en un procés o càlcul determinat.
Així, el centre de masses d’un cos s’anomena també centre d’atracció En la teoria de la iteració apareixen punts o conjunts de punts on convergeixen determinats resultats iteratius i per això s’anomenen atractors
correspondència
Matemàtiques
Una correspondència entre dos conjunts A
i B
és definida com un subconjunt del producte cartesià A × B
.
És fàcil de relacionar aquesta definició amb la idea intuïtiva de correspondència per exemple, si A és el conjunt dels països, i B el dels idiomes, la correspondència tal idioma es parla a tal país determina exactament un subconjunt de A × B el de les parelles a, b tals, que en el país a es parla l’idioma b En una correspondència el conjunt d’elements de A que apareixen com a primers elements de parelles de la correspondència és anomenat domini , i el conjunt d’elements de B que apareixen com a segons elements en les parelles de la…
signatura
Matemàtiques
Nombre de termes positius en una forma quadràtica reduïda a una suma de quadrats mitjançant una transformació lineal.
La signatura d’una matriu simètrica és el nombre de termes positius que apareixen en diagonalitzar la matriu Amb el rang , la signatura constitueix un dels invariants fonamentals en la classificació de les matrius corresponents a les còniques i a les quàdriques
aràbic | aràbiga
Matemàtiques
Dit dels signes gràfics del sistema de numeració posicional i decimal utilitzats als països occidentals actualment (numeració, xifra).
Sembla que aquests signes eren d’origen indi i foren el model de les xifres dels àrabs occidentals, més semblants a les índies que no pas les dels àrabs orientals Sembla cert que, a través de Còrdova, foren conegudes a Catalunya a la segona meitat del segle X Consta que Gerbert el futur papa Silvestre II les aprengué durant la seva estada a Vic, Girona i Barcelona, entre el 967 i el 970 Les figuracions més antigues conegudes entre els llatins són les dels còdexs Albeldense i Emilianense ara a El Escorial, escrits el 976 i el 994 respectivament Només consten de nou xifres en ordre invers, és a…
grup
Matemàtiques
Estructura algèbrica constituïda per un conjunt G on hi ha definida una operació, designada per *, que per a qualssevol elements a, b, c de G té aquestes tres propietats: propietat associativa, o sia (a*b) *C = a*(b*c); G conté un element neutre e, o sia a*e = a; i per a qualsevol element a n’hi ha un altre de G, representat per a’, que és el seu invers (a*a’ = a’*a = e).
Si a més es compleix la propietat commutativa a*b = b*a , el grup és anomenat commutatiu o abelià i, en aquest cas, si hom representa l’operació amb el signe +, el grup és anomenat també additiu , mentre que si hom utilitza el signe o uns altres, el grup és anomenat també multiplicatiu Hom anomena ordre d’un grup el nombre d’elements que conté més exactament, és el cardinal del conjunt dels seus elements El grup és anomenat cíclic si qualsevol element s’obté per producte repetit d’un de fix, anomenat generador L’estudi en abstracte dels grups permet d’obtenir resultats aplicables a grups…