Resultats de la cerca
Es mostren 8 resultats
bisector
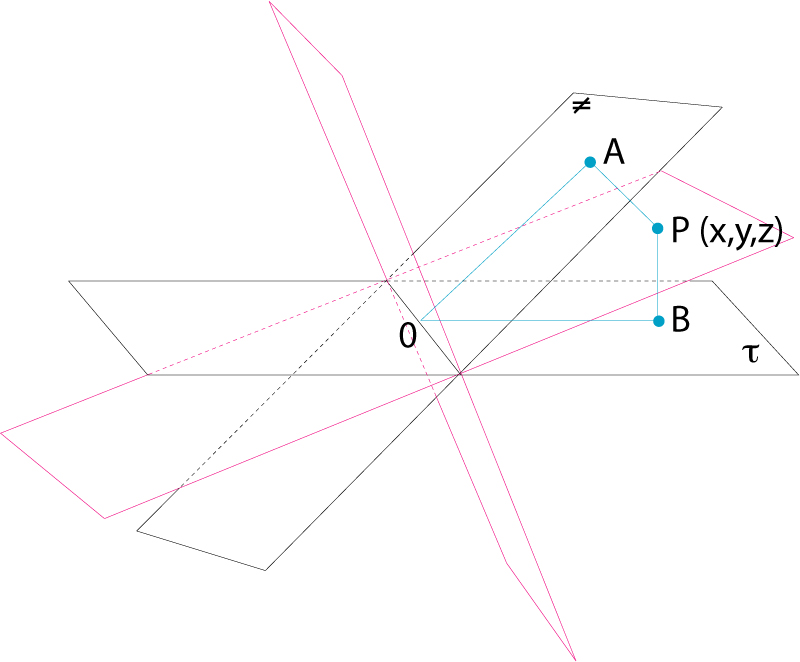
Plans bisectors dels quatre díedres formats per dos plans donats que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels dos plans costats d’un angle díedre, el qual, per tant, és dividit en dos díedres iguals.
Dos plans no parallels determinen quatre angles díedres, per als quals hom distingeix dos plans bisectors Per a cada díedre, un dels plans bisectors serà interior, i l’altre, exterior Si les equacions cartesianes de dos plans són A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0, en una referència cartesiana normal, l’equació dels dos plans bisectors dels díedres que aquells determinen és
objecte matemàtic
Matemàtiques
Concepte matemàtic precisat per una definició.
El caràcter matemàtic de l’objecte és donat per la possibilitat d’establir relacions entre aquest i els altres objectes de la teoria, en forma de teoremes, els quals hom dedueix dels axiomes de partença Sovint els objectes matemàtics són classes d’equivalència construïdes a partir d’altres elements anteriors concepte de nombre enter, de direcció, de vector lliure, etc Hom anomena objectes primitius d’una teoria matemàtica aquells que no poden ésser definits a partir d’objectes anteriors i han d’ésser definits establint una sèrie de condicions que els relacionen entre ells, com és…
cònica
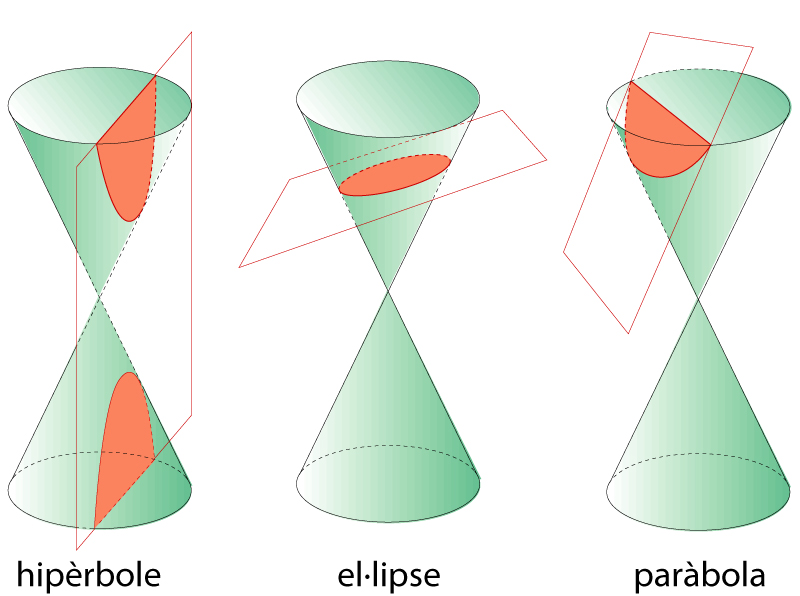
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
configuració
Matemàtiques
Terme de gran abast que designa tots aquells objectes matemàtics que consisteixen, bàsicament, en un conjunt finit d’elements i en una família de parts del conjunt, ambdós satisfent unes certes condicions de regularitat algèbriques o topològiques.
Són configuracions objectes tan distints com les variacions, les combinacions o les permutacions d’un conjunt d’elements, o com les diferents disposicions de paquets de mides desiguals en l’interior d’una maleta
teoria de la computació
Matemàtiques
Branca de les matemàtiques que estudia problemes de decidibilitat.
Com és usual en la història de les matemàtiques, té orígens aparentment molt diferents que finalment conflueixen i permeten d’establir el que esdevé una teoria enormement potent i irrenunciable Cal remarcar-ne el problema diofàntic plantejat per David Hilbert l’any 1900, i el problema de les paraules que sorgí en el món de la topologia algèbrica Es tracta de dos problemes típics de decidibilitat és a dir, aquells en què cal disposar d’un mètode que permeti de decidir una o altra de dues opcions atesa una equació diofàntica, té solució, són equivalents dues paraules donades per endavant L’any…
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats topològiques a aquells…
estadística
Matemàtiques
Ciència, mètode, tècniques, operació d’anàlisi matemàtica, que permeten d’estudiar numèricament amb el màxim de precisió els fenòmens col·lectius incompletament coneguts.
Molt abans que les dades provinents d’observacions poguessin ésser estudiades rigorosament i científicament, els estats havien organitzat, amb més o menys cura, la recollecció pretesament exhaustiva de dades amb fins diversos, principalment per a les lleves militars i els imposts És ben conegut el cens ordenat pels romans l’any 0 hom coneix, també l’existència d’elaboració de censos fa uns 4 000 anys a la Xina, i la Bíblia n'esmenta diversos en el llibre dels Nombres L’estadística permet a l’administració de conèixer la situació de les persones i dels béns que hi ha sota llur jurisdicció…
aritmètica
Matemàtiques
Estudi dels nombres naturals i de les operacions d’addició, subtracció, multiplicació, divisió entera, potenciació i extracció d’arrels enteres entre aquests nombres.
L’aritmètica ha nascut a totes les civilitzacions ensems amb el llenguatge per anomenar conjunts de persones o d’objectes i després per facilitar els intercanvis comercials Els egipcis s’havien ocupat d’alguns problemes aritmètics, i les obres que n'han estat conservades la més antiga de les quals és el papir Rhind ~s XVII aC contenen la resolució d’algunes qüestions numèriques sense dir en quines propietats recolza la resolució, ni menys encara justificar-les El nivell de llurs coneixements era, aproximadament, el de l’actual ensenyament primari, però eren enunciats amb un llenguatge més…