Resultats de la cerca
Es mostren 16 resultats
cònica
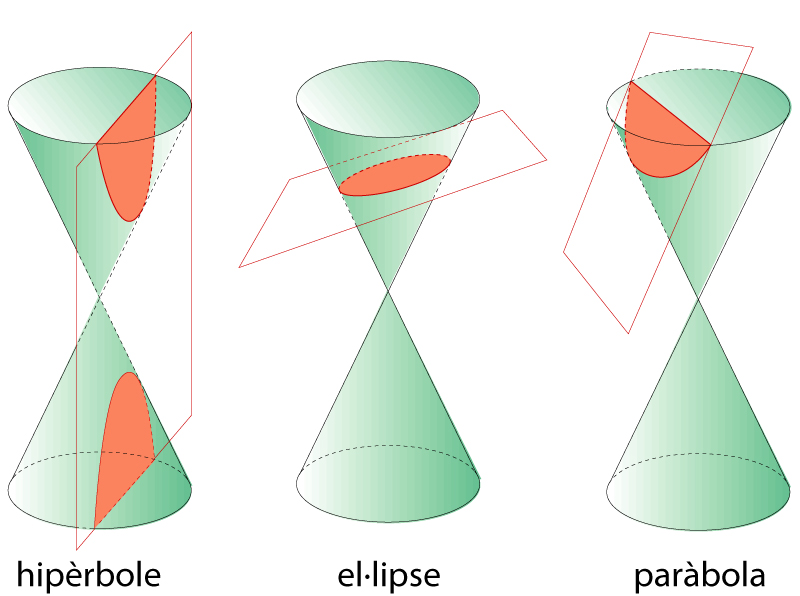
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la…
Aristeu de Crotona
Matemàtiques
Matemàtic grec.
Escriví cinc llibres sobre Els llocs sòlids on formulà teoremes sobre els cinc sòlids regulars i sobre les corbes còniques Influí sobre Euclides, bé que el tractat d’Aristeu és més important i original Les seves obres només són conegudes per referències de Pappus i Euclides Això fa que tota l’originalitat de l’estudi de les còniques recaigui sobre Apolloni de Perge
con
Matemàtiques
Superfície reglada generada per totes les rectes (generatrius) que passen per un punt dit vèrtex i per una corba (exterior al punt donat) dita directriu.
La superfície consta de dos fulls units pel vèrtex Es parla de con de revolució si la superfície cònica és engendrada per una recta que passa pel vèrtex i gira al voltant d’una altra recta que també hi passa, la qual és anomenada eix del con Les corbes obtingudes en tallar un con de revolució amb un pla que no passa pel vèrtex reben el nom de seccions còniques o, simplement, còniques Si el pla secant és parallel a una generatriu del con, la cònica rep el nom de paràbola en la resta de casos, el pla secant determina una ellipse o una hipèrbola, segons si el pla…
focus
Matemàtiques
Punt la distància del qual a qualsevol dels punts d’una corba pot ésser expressada com una funció racional de les coordenades dels punts.
Aquesta definició mètrica de focus, que és una generalització dels focus de les còniques cònica, no permet, però, d’ésser estesa a una corba algèbrica qualsevol, i per aconseguir-ho cal passar a la definició projectiva de focus
Michel Chasles
Matemàtiques
Matemàtic francès.
Fou professor de geodèsia i mecànica aplicada a l’escola politècnica, i de geometria superior a la Sorbona Creà la geometria projectiva moderna independentment de Jakob Steiner Autor de Traité de géométrie supérieure 1852 i Traité des sections coniques 1865
signatura
Matemàtiques
Nombre de termes positius en una forma quadràtica reduïda a una suma de quadrats mitjançant una transformació lineal.
La signatura d’una matriu simètrica és el nombre de termes positius que apareixen en diagonalitzar la matriu Amb el rang , la signatura constitueix un dels invariants fonamentals en la classificació de les matrius corresponents a les còniques i a les quàdriques
secció
Matemàtiques
Intersecció d’un pla amb una superfície.
Si aquesta és una superfície cònica, hom parla de seccions còniques ellipses, hipèrboles i paràboles, parells de rectes, etc Les seccions produïdes en prismes i cilindres per plans perpendiculars, respectivament, a les arestes laterals i a les generatrius, són anomenades seccions rectes
Colin Maclaurin
Matemàtiques
Matemàtic escocès.
A la seva obra fonamental, A Treatise of Fluxions 1742, prolongà amb mètodes originals els càlculs del seu mestre INewton sobre determinades qüestions encara no aclarides del tot, com la figura d’equilibri d’una massa fluida en rotació, l’atracció exercida per un ellipsoide homogeni sobre punts de la seva superfície o el seu interior, etc Establí també la fórmula que duu el seu nom, sobre el desenvolupament en sèrie de funcions És autor de Geometria organica 1719, i descobrí un nou mètode de descripció de les còniques
Hipàcia
Matemàtiques
Matemàtica, metgessa i filòsofa.
Escrigué un comentari als sis primers llibres de l' Aritmètica de Diofant i també un tractat sobre les Còniques d' Apolloni El seu pare fou Teó d'Alexandria , prestigiós matemàtic i astrònom, del qual aprengué els descobriments astronòmics de Ptolemeu Es preocupà d’editar l' Almagest , l’obra més important d’aquest insigne astrònom grec Fou una defensora indiscutible de la filosofia neoplatònica i s’oposà a la implantació del cristianisme al Museu d’Alexandria, del qual fou el darrer director Morí assassinada al carrer en mans de cristians fanàtics en veure que no volia…