Resultats de la cerca
Es mostren 10 resultats
bruixa d’Agnesi
bruixa d’Agnesi
© Fototeca.cat
Matemàtiques
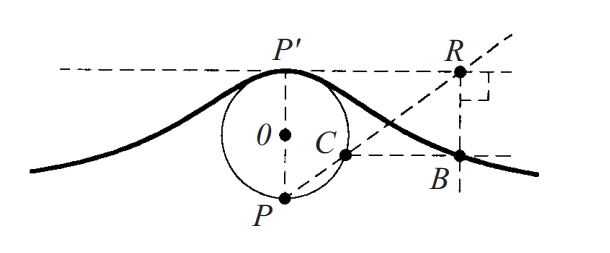
Cúbica plana generada a partir d'una circunferència, un punt P d'aquesta i la tangent en el punt diametralment oposat a P.
Cada recta traçada per P talla la circumferència en un punt C , i la tangent en un punt R La corba és el lloc dels punts d'intersecció de la perpendicular per R a la tangent amb la parellela a aquesta tangent traçada des de C
funció polinòmica
Matemàtiques
Donat un polinomi a0 + a1 X + ... + anXn , funció f(x) que fa l’assignació x → a0 + a1x + ... + anxn.
El grau n del polinomi és el grau de la funció polinòmica Quan n = 2 la funció és quadràtica i quan n = 3 és cúbica
cissoide de Diocles
cissoide de Diocles
Matemàtiques
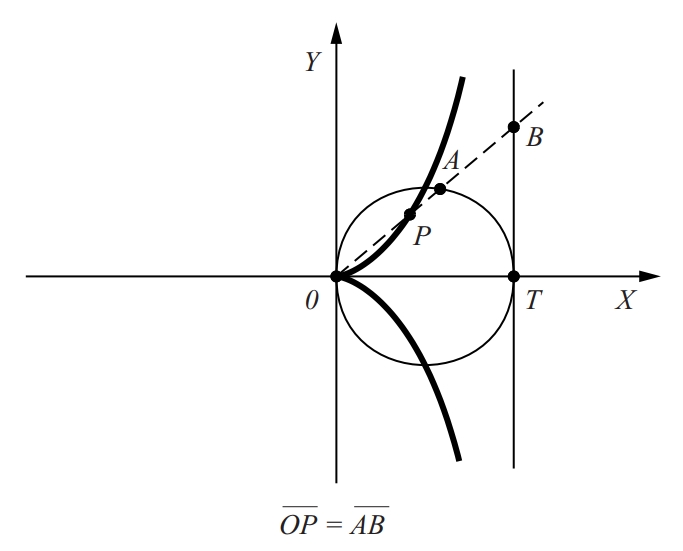
Cissoide associada amb una circumferència, a una recta tangent i a un punt fix O diametralment oposat al punt de tangència.
Fou construïda per Diocles per resoldre la duplicació del cub La seva equació cartesiana és y 2 2 k – x = x 3 Es tracta, doncs, d’una cúbica
resolvent
Matemàtiques
Donada una equació de quart grau amb solucions x1, x2, x3, x4 , equació de tercer grau que té com a solucions (x1+x2 ) · (x3+x4 ), (x1+x3 )·(x2+x4 ) i (x1+x4 )·(x2+x3 ).
Si l’equació de quart grau és de la forma x 4 +px 2 +qx+r = 0 la seva resolvent és y 3 -2py 2 + p 2 -4r y + q 2 = 0 A partir de les solucions d’aquesta equació cúbica hom n'obté fàcilment les de l’equació original
estrofoide
Estrofoide
© fototeca.cat
Matemàtiques
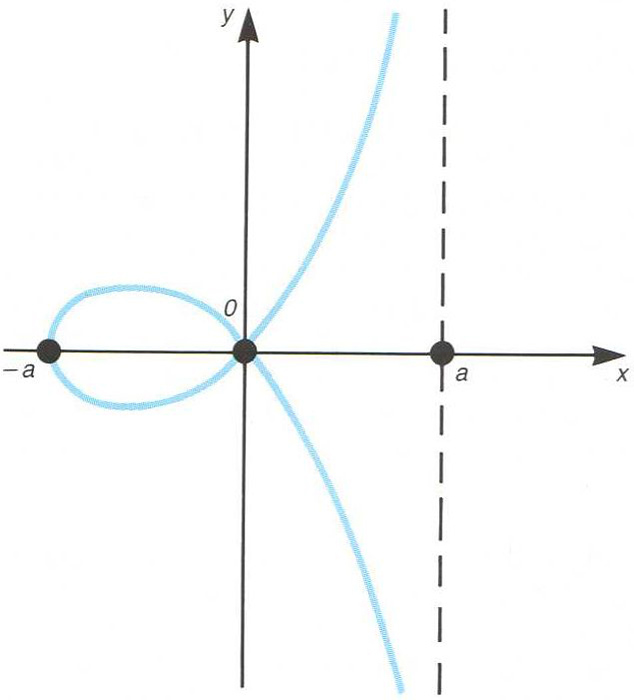
Corba plana, cúbica circular d’equació cartesiana
y 2
( a-x
) =
x 2
( a+x
), a
>0.
L’origen és un punt doble L’equació en coordenades polars és r = - a cos 2ϑ/cos ϑ La línia x = a n'és una asímptota
foli de Descartes
Foli de Descartes
© fototeca.cat
Matemàtiques
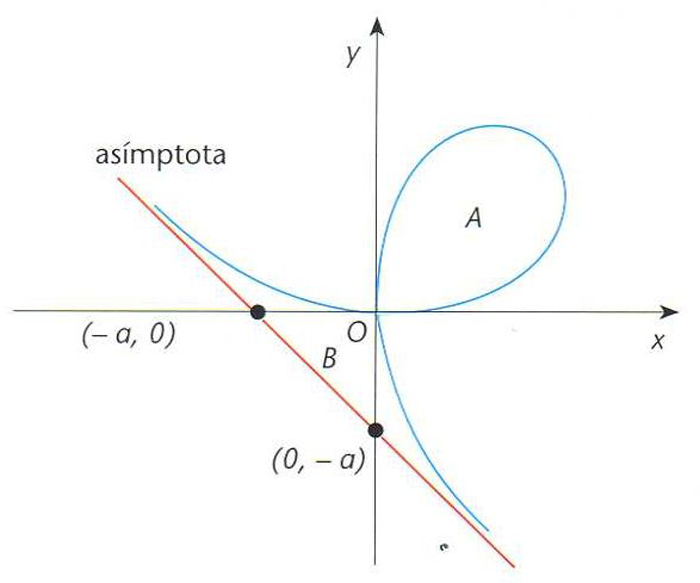
Cúbica expressada implícitament per l’equació cartesiana x3+y3=3axy, on a és una constant.
En forma paramètrica és expressada per x=3at|1+t 3 i y=3at 2 |1+t 3 La recta traçada pels punts de coordenades - a , 0 i 0, -a és una asímptota de la corba L’àrea A limitada pel llaç és igual a l’àrea B compresa entre les dues branques infinites i la asímptota esmentada
arrel
Matemàtiques
Quantitat x que, presa com a factor un cert nombre de vegades n, dóna com a producte una quantitat determinada a.
Hom ho expressa amb on a és el subradicand, x l’arrel i n l’índex aquesta expressió equival a x n = a El signe √sembla provenir de la deformació de la r inicial del mot llatí radix , ‘arrel’ àlgebra Una arrel d’índex 2 és anomenada arrel quadrada hom acostuma a suprimir gràficament l’índex d’índex 3, arrel cúbica d’índex 4, arrel biquadrada Les arrels de qualsevol altre índex no reben cap nom específic L’existència d’una arrel enèsima d’índex n q de p, on q i p són nombres reals i positius, és demostrada pel fet que la funció y = x n , on x varia de 0 a + ∞, és contínua i,…
serpentina
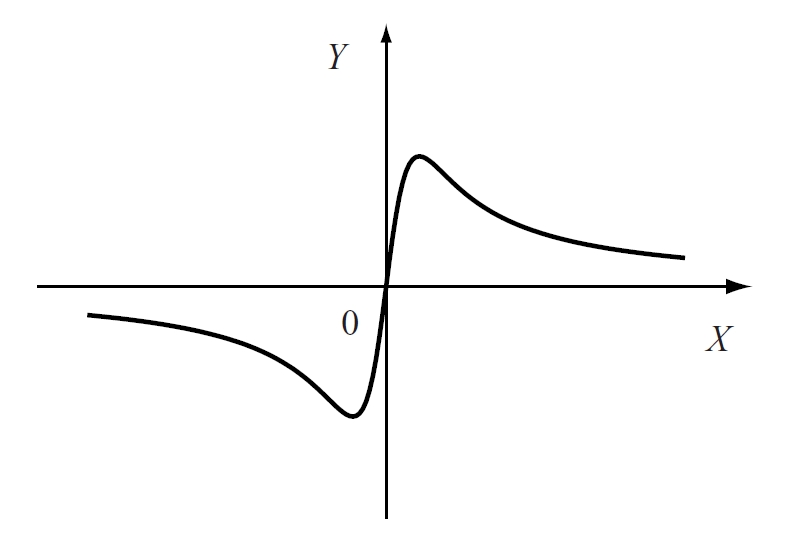
serpentina
Matemàtiques
Corba cúbica plana d’equació x2y + a2y – b2x = 0 que és la projecció de l’horòptera.