Resultats de la cerca
Es mostren 8 resultats
ròmbic | ròmbica
prismàtic | prismàtica
Lotfi A. Zadeh

Lofti A. Zadeh
© Franklin Institute Awards
Matemàtiques
Matemàtic nord-americà d’origen azerbaidjanès.
Estudià a Teheran enginyeria elèctrica El 1944 s’installà als EUA i estudià al Massachusetts Institute of Technology i a la Columbia University, on es doctorà el 1949 Fou professor d’aquesta universitat i, posteriorment, de la University of California, on dirigí el Berkeley Initiative for Soft Computing Feu notables contribucions a la teoria dels sistemes, exposades en l’obra Linear System Theory 1963, amb CA Desoer El 1964 introduí el mètode anomenat dels conjunts difusos , per tal de tractar d’una manera matematicooperativa la vaguetat associada a la parla habitual, teoria que …
complement d’una part d’un conjunt
Matemàtiques
Donada una part A
d’un conjunt C, A ⊂C,
subconjunt de C
format pels elements de C
que no pertanyen a A
; és representat per CA
.
De manera menys precisa, hom pot definir també el complement d’un conjunt qualsevol C , com el complement del conjunt respecte al conjunt universal format per tots els possibles elements de tots els possibles conjunts, és a dir, el complement de C és el conjunt C' tal que C ∪ C' = U i C ∩ C' = ∅on U és el conjunt universal
teorema de Menelau
teorema de Menelau
© fototeca.cat
Matemàtiques
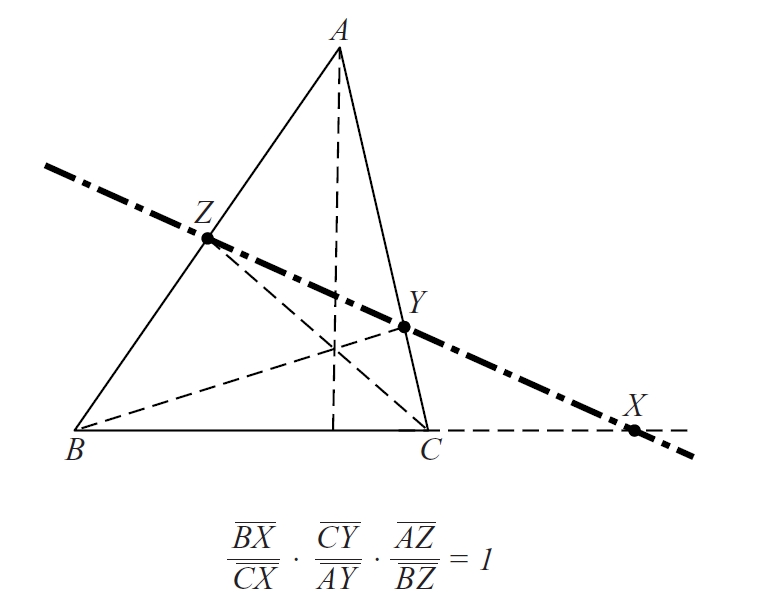
Teorema segons el qual tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB, respectivament, d’un triangle ABC, estan alineats si, i solament si, (BX⁄CX)·(CY⁄AY)·(AZ ⁄ BZ) = 1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui +1 X , A , B Y , B , C Z , C , A = 1 Aquest teorema és dual del teorema de Ceva
teorema de Desargues
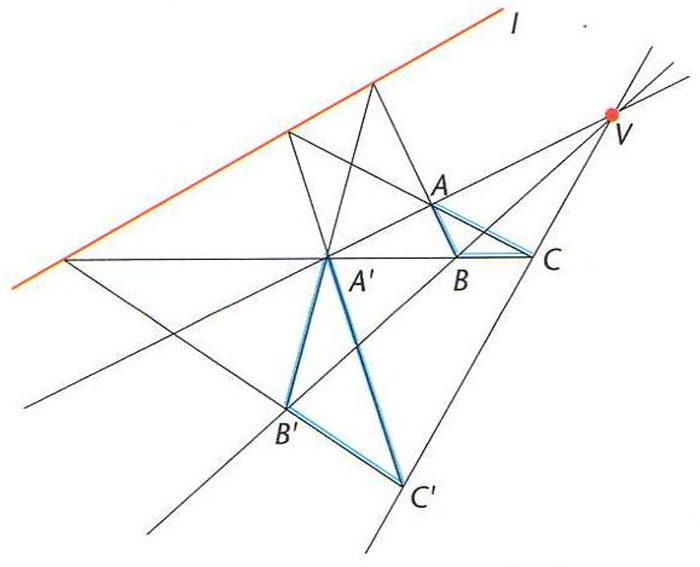
V és el punt de concurrència de les rectes AA’, BB' i CC' i l és la línia que conté els punts de concurrència de AB i A'B', de BC i B'C' i de CA i C'A'
© fototeca.cat
Matemàtiques
Teorema segons el qual, donats dos triangles ABC i A’B’C’ tals que les rectes AA’, BB’ i CC’ són concurrents, els punts de concurrència de AB i A’B’, de BC i B’C’ i de CA i C’A’ són alineats.
teorema de Ceva
teorema de Ceva
Matemàtiques
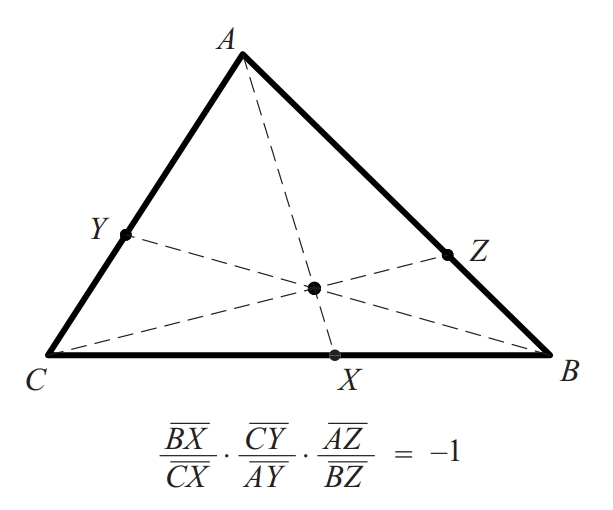
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar…