Resultats de la cerca
Es mostren 37 resultats
covariant
Matemàtiques
Dit dels tensors d’ordre superior a 1 les components dels quals es transformen, en un canvi de coordenades, segons la matriu del canvi de base.
Per exemple, si és un canvi de base de l’espai vectorial en qüestió, les components d’un vector v covariant es transformen com Les components o coordenandes d’un vector covariant són indexades mitjançant subíndexs v μ
contravariant
Matemàtiques
Dit dels tensors d’ordre superior a 1 les components dels quals es transformen, en un canvi de coordenades, segons la matriu inversa del canvi de base.
Per exemple, si e ' v = A µ v e µ és un canvi de base de l’espai vectorial en qüestió, les components d’un vector v contravariant es transformen com v ' µ = A - 1 µ v v Les components o coordenades d’un vector contravariant són indexades mitjançant superíndexs v µsup
transposició
Matemàtiques
En una matriu, canvi de les files per les columnes.
Així, la matriu es transforma per transposició en El determinant d’una matriu quadrada és invariant per transposició Una matriu en què la inversa és igual a la transposada, és anomenada ortogonal aquestes matrius representen els moviments lineals que conserven distàncies, angles i productes escalars
normalització
Matemàtiques
Canvi d’escala que fa que una suma o una integral tingui un valor unitat.
La normalització és assolida, generalment, mitjançant l’ajust d’una constant arbitrària
monàdic | monàdica
Matemàtiques
Dit d’una operació amb un sol operand, com, per exemple, el canvi de signe.
compàs de reducció
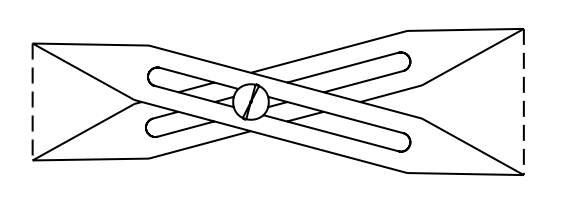
compàs de reducció
Matemàtiques
Compàs que permet passar d’una mida a una altra de proporcional (canvi d’escala).
diagonalitzar
Matemàtiques
Convertir en forma diagonal (la matriu d’un endomorfisme d’un espai vectorial) mitjançant un canvi de base.
element infinitesimal
Matemàtiques
Element que, en valor absolut, és més petit que qualsevol nombre real estàndard i, en canvi, és no nul..
És la base conceptual de l’anàlisi no estàndard, intuïda per Wilhelm Gottfried Leibniz al segle XVII i, formalitzada per Abraham Robinson al començament dels anys seixanta, usa tècniques de teoria de models
diagonalització
Matemàtiques
Conversió en forma diagonal de la matriu d’un endomorfisme d’un espai vectorial, mitjançant un canvi de base.
Per tal que la diagonalització sigui possible és necessari i suficient que hi hagi una base de l’espai formada per vectors propis o autovectors de l’endomorfisme