Resultats de la cerca
Es mostren 16 resultats
compàs de reducció
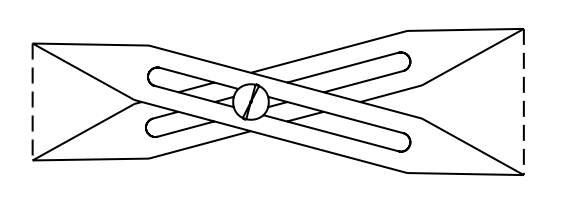
compàs de reducció
Matemàtiques
Compàs que permet passar d’una mida a una altra de proporcional (canvi d’escala).
el·lipsògraf
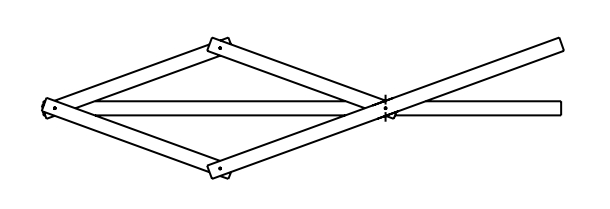
El·lipsògraf de quadrants
rectificació
Matemàtiques
Determinació de la longitud d’una corba o d’un arc d’aquesta.
Hom pot provar que la rectificació d’una circumferència és impossible de fer gràficament mitjançant el regle i el compàs
nombre primer de Gauss
Matemàtiques
Cadascun dels nombres primers que poden ésser expressats per la fórmula 22n + 1.
Gauss els emprà en estudiar les possibles divisions del cercle, i arribà a la conclusió que hom pot construir amb regle i compàs tot polígon regular amb un nombre primer 2 2 n + 1 de costats
trisecció d’un angle

Trisecció d’un angle, mitjançant la "destral índia"
Matemàtiques
Divisió d’un angle en tres angles iguals.
La trisecció d’un angle constituí un dels problemes clàssics, i hom demostrà que és insoluble gràficament mitjançant el regle i el compàs per a la solució cal emprar corbes d’ordre superior al segon, com la concoide de Nicomedes
quadratura del cercle
Matemàtiques
Operació consistent a trobar, mitjançant mètodes geomètrics, un quadrat d’igual àrea que la d’un cercle donat.
Això, que constituí un cèlebre problema clàssic, ha estat resolt modernament, gràcies a l’obra de Galois essencialment, perquè ha estat demostrat que aquest problema no té solució hom ha demostrat la impossibilitat de construir amb regle i compàs un segment de longitud π a partir d’un segment unitat La quadratura del cercle només és possible amb l’ús de corbes transcendents especials anomenades quadratrius
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats
cos
Matemàtiques
Conjunt dotat de dues operacions, que hom acostuma a designar + i × (suma i producte), amb les següents propietats: respecte a la suma el conjunt té estructura de grup commutatiu, i també amb el producte és grup, commutatiu o no, i segons això el cos es dirà d’una manera o d’una altra.
A més, hom exigeix que l’operació × tingui la propietat distributiva respecte a la + Hom pot dir, doncs, que un cos és un anell tal, que cada element té invers respecte a l’operació × Un cos té només dos ideals el 0 i ell mateix Els exemples més immediats són el cos ℝdels nombres reals, amb les operacions usuals de suma i producte, el cos ℚdels nombres racionals i el ℂdels complexos Hi ha el cos de dos elements 0 i 1, amb les operacions + 0 element neutre 1 + 1 = 0, i × habitual Com a exemple de cos no commutatiu hi ha el dels quaternions La característica d’un cos és el nombre més petit p…
pi
Matemàtiques
Lletra grega, inicial del mot grec περιφέρεια (‘circumferència’)..
És adoptada per a representar la raó constant que existeix entre la longitud de la circumferència i el seu diàmetre longitud de la circumferència, 2πR àrea del cercle, πR 2 àrea de l’esfera, 4πR 2 volum de l’esfera, L’ús d’aquesta llegra grega per a designar la relació entre la longitud de la circumferència i el seu diàmetre es remunta solament al s XVII, i es generalitzà a partir de la publicació de l’obra d’Euler Introductio in analysim infinitorum el mateix Euler i JBernoulli usaren P i c , respectivament, com a símbol representatiu A Egipte hom havia fet aproximacions empíriques del…
obertura
Matemàtiques
Grau de divergència dels costats d’un angle, d’un compàs, etc.