Resultats de la cerca
Es mostren 19 resultats
nombre concret
Matemàtiques
Nombre no abstracte, és a dir, que expressa la quantitat d’una determinada cosa.
univers
Matemàtiques
Conjunt de referència els subconjunts del qual són utilitzats en un raonament concret.
En els diagrames de Venn-Euler hom sol representar l’univers amb un rectangle, dins el qual són dibuixats els diagrames dels conjunts que hom vol representar Així, en l’estudi dels conjunts de nombres reals l’univers és ℝ
teoria de categories
Matemàtiques
Teoria introduïda cap al 1940 pels matemàtics S. Eilenberg i S. MacLane, fonamentada sobre el concepte de categoria, i aplicada inicialment en la topologia algèbrica.
És utilitzada en tot aquell tipus de problema algèbric on hom té una estructura de base i un conjunt de propietats genèriques que no depenen de la realització en un objecte matemàtic concret, especialment en àlgebra homològica i geometria algèbrica
càlcul diferencial
Matemàtiques
Part de l’anàlisi matemàtica, i, més concretament, de l’anàlisi infinitesimal, que tracta de totes les qüestions relacionades amb els conceptes fonamentals de derivada (ordinària o parcial) i de diferencial d’una funció.
Hom el considera com una teoria conceptual estesa també com a tècnica de càlcul que permet de traduir les propietats geomètriques i físiques de l’espai en forma analítica, independentment del sistema de coordenades concret al qual hom ha referit l’espai
condicions inicials
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui, ella i les seves derivades, uns determinats valors per a un valor especificat de la variable independent.
Les condicions inicials permeten, doncs, de determinar la solució particular del problema en ajustar les constants arbitràries de la solució general Per exemple, en el problema del moviment d’una massa puntual, un cop conegudes les forces que hi actuen, el moviment concret que realitza depèn només de la posició i la velocitat en un instant inicial, x t o i v t o , essent aquestes les condicions inicials del problema
mètode de reducció a la unitat
Matemàtiques
Mètode que permet de resoldre els problemes de proporcionalitat reduint-los al cas en què la quantitat a què és proporcional la incògnita té el valor de la unitat.
L’aplicació d’aquest mètode a un problema senzill concret és la següent Si sabem que algú recorre 15 km en 3 hores i volem saber quin ha estat el camí recorregut en 2 hores, hom raona així recorre 15/3 km/h = 5 km/h, i, per tant, el camí recorregut en dues hores és 5 x 2 = 10 km El mètode de reducció a la unitat representa una alternativa racional a la regla de tres
efectiu
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, nombre d’individus que presenten un valor concret del caràcter.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,, x n , sobre una mostra de N individus, l’efectiu del valor x i és el nombre d’individus de la mostra que presenten el valor x i del caràcter Si el caràcter quantitatiu és continu , donada una classe o interval del conjunt de valors del caràcter C i = a i - 1 ,a i , l’efectiu de la classe és el nombre d’individus que presenten un valor del caràcter que pertany a la classe
el·lipse
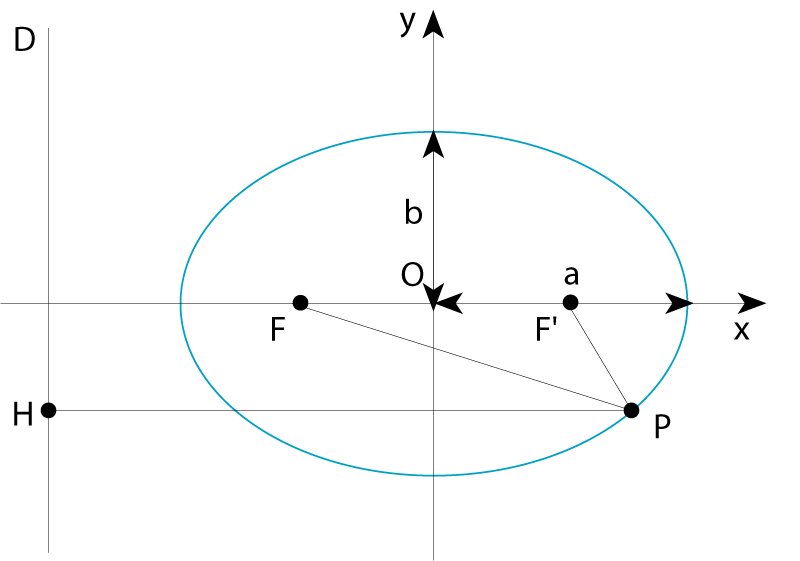
El·lipse de semieixos a i b; D és la directriu associada al focus F
© Fototeca.cat
Matemàtiques
Corba tancada que resulta de la intersecció d’una superfície cònica amb un pla que no és paral·lel a cap generatriu ni a l’eix d’aquella; és doncs, una cònica
.
La seva equació en coordenades cartesianes referides als seus dos eixos perpendiculars de simetria és x 2 / a 2 + y 2 / b 2 =1, a essent el semieix major i b el semieix menor L’ellipse és el lloc geomètric dels punts P del pla tals que la suma de llurs distàncies a dos punts fixos F i F ´, anomenats focus , és una quantitat constant, independent del punt P concret, igual al doble del semieix major, PF + PF ´=2 a és també el lloc geomètric dels punts P tals que el quocient de llurs distàncies a un punt fix, un dels focus, i a una recta fixa D , anomenada directriu , és una…
autòmat finit
Matemàtiques
Electrònica i informàtica
Model matemàtic d’un sistema que té un nombre finit d’estats d’entrada i de sortida —els quals representen les diferents configuracions de signes (i estats interns) que representen la capacitat que té el sistema d’enregistrar els esdeveniments passats— i en el qual l’estat de sortida depèn en qualsevol moment de l’entrada present i dels estats interns.
Per tant, un autòmat finit es defineix pel conjunt finit dels estats d’entrada, de sortida i interns possibles per una funció que dóna el següent estat intern corresponent a un estat d’entrada i a un estat intern donats i per una funció que determina l’estat de sortida següent Aquest concepte és essencialment abstracte i té valor tant per a descriure programes com per a descriure aparells Un autòmat finit concret es defineix normalment per mitjà de la seva taula d’estats , que consisteix en una llista de les relacions existents entre els estats d’entrada, els de sortida i els…